Chapitre 3 : Nombre dérivé et tangente

Chapitre 3 : Nombre dérivé et tangente
I
Rappels sur les droites
I.1
Tracer une droite connaissant une équation
Exercice 1
1
Tracer les droites (d1 ) : y = x − 3, (d2 ) : y = 2, et (d3 ) : x = −4.
2
Remarque
Les droites d’équation y = k son parallèles à l’axe des abscisses.
Les droites d’équation x = k sont parallèles à l’axe des ordonnées. Ce ne sont pas
des représentations graphiques de fonctions, elles n’ont pas de coefficient directeur.
I.2
Calculer ou lire un coefficient directeur à partir de 2
points
Propriété
Soient A(xA ; yA ) et B(xB ; yB ) deux points dans un repère, avec xA 6= xB .
yB − yA
.
Le coefficient directeur de la droite (AB) est m =
xB − xA
Exercice 2
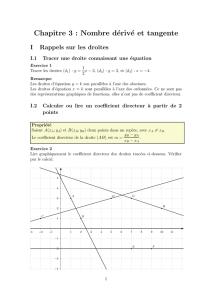
Lire graphiquement le coefficient directeur des droites tracées ci-dessous. Vérifier
par le calcul.
a
d
5
4
A
3
G
D
b
b
b
H
b
2
B
C
1
b
−3
−2
b
1
−1
2
3
4
5
6
7
8
9
10
−1
E
b
−2
−3
−4
1
F
b
11
Réponses : Le coefficient directeur de la droite (AB) est m = −2.
2
Le coefficient directeur de la droite (CD) est .
7
Le coefficient directeur de la droite (EF ) est 0.
1
Le coefficient directeur de la droite (GH) est − .
3
II
Nombre dérivé, tangente
Définition
Soit f une fonction définie sur un intervale I. On note C sa courbe représentative
dans un repère du plan. Soit a ∈ I.
On appelle nombre dérivé de f en a, s’il existe, le coefficient directeur de la tangente
à C au point d’abscisse a. On le note f ′ (a).
Exemple : on a représenté la fonction carré définie par f (x) = x2 .
4
b
A
3
b
D
2
b
1
B
b
−4
−3
−2
C
−1
1
2
3
4
5
−1
−2
1. On a tracé la tangente à C au point A(−2; 4), c’est la droite (AC).
A est le point d’abscisse −2.
Donc f ′ (−2) est le coefficient directeur de la droite (AC).
On lit sur le graphique A(−2; 4) et C(−1; 0).
0−4
yC − yA
=
= −4.
xC − xA
−1 − (−2)
On en déduit que f ′ (−2) = −4.
2. La droite (BD) est la tangente à la courbe au point B d’abscisse 1.
f ′ (1) est le coefficient directeur de la droite (BD).
f ′ (1) = 2.
Remarque
— Une fonction f est dérivable en a si sa courbe admet en a une tangente non
parallèle à l’axe des ordonnées.
2
— On retiendra que f ′ (a) est le coefficient directeur de la tangente à la courbe
au point d’abscisse d’abscisse a.
Exercice 3
On a tracé la courbe C d’une fonction f et la tangente à la courbe C au point A.
C
2
b
B
b
1
−2
1
−1
2
3
4
5
6
7
8
−1
A
−2
b
−3
−4
1. Déterminer f ′ (1). Justifier.
2. La tangente au point C est parallèle à l’axe des abscisses. En déduire un
nombre dérivé de f .
3. On admet que f ′ (4) = −2. Tracer la tangente à la courbe de f au point
d’abscisse 4. Expliquer la construction.
Remarque (Cas particulier à retenir)
Soit f une fonction dérivable en a.
f ′ (a) = 0 ssi la tangente à la courbe au point d’abscisse a est parallèle à l’axe des
abscisses.
III
Fonction dérivée
Définition
Soit f un fonction définie sur un intervalle I.
On dit que f est dérivable sur I si f admet un nombre dérivé en tout réel de I,
c’est-à-dire si pour tout x ∈ I, f ′ (x) existe.
Alors, on appelle la fonction dérivée de f la fonction f ′ qui à tout réel x de I associe
le nombre dérivé f ′ (x).
3
III.1
Dérivées des fonctions usuelles
Théorème (à connaı̂tre par ♥)
Fonction f
Dérivée f ′
Intervalle de validité
f (x) = c (fonction constante)
f (x) = x
f (x) = ax + b
f ′ (x) = 0
f ′ (x) = 1
f ′ (x) = a
I=R
I=R
I=R
f (x) = x2
f (x) = ax2 + bx + c
f ′ (x) = 2x
f ′ (x) = 2ax + b
I=R
I=R
f (x) = x3
f (x) = xn n > 1
f ′ (x) = 3x2
f (x) = nxn−1
I=R
I=R
f (x) =
1
x
f (x) =
√
III.2
f ′ (x) = −
x
1
x2
1
f ′ (x) = √
2 x
I =] − ∞; 0[ ou ]0; +∞[
I =]0; +∞[
Opérations sur les fonctions dérivables
Théorème
Soient u et v des fonctions dérivables sur un intervalle I. Alors :
1. Somme de fonctions.
La fonction (u + v) est dérivable sur I et (u + v)′ = u′ + v ′ .
2. Différence de fonctions.
La fonction (u − v) est dérivable sur I et (u − v)′ = u′ − v ′ .
3. Produit par un nombre réel.
Soit k ∈ R (une constante).
La fonction (k × u) est dérivable sur I et (k × u)′ = k × u′ .
4
Exemple :
2
f (x) = 5x3 + .
x
2
−1
′
f (x) = 5 × 3x2 + 2 × 2 = 15x2 − 2 .
x
x
5