Document

1
1S DEVOIR COMMUN (2h) 11/01/2010
Calculatrice INTERDITE
Exercice 1 :
Résoudre l’équation :
2sin 1 0
x
+ =
[ ]
[ ]
)
) 0; 2
) ;
a
b
c
π
π π
−
Exercice 2 :
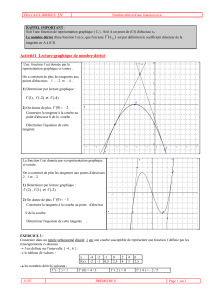
Sur la figure ci-contre, M et N sont tels que : OM=3 ON=4 ( ; )
3
i OM
π
=
( ; )
4
i ON
π
= −
.
De plus,
2
OA i j
= − −
et
2 2
OB i j
= − +
.
1. Quelles sont les coordonnées polaires des points M et N ?
2. Calculer les coordonnées polaires du point B. En déduire que O, B et N
sont alignés.
3. Utiliser les coordonnées cartésiennes des points A et M pour prouver
que O, A et M ne sont pas alignés.
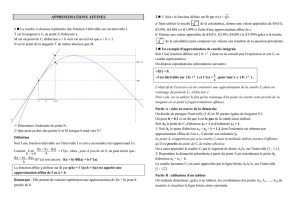
Exercice 3:
On présente ci-contre la courbe représentative d’une fonction
f
et quatre de ses tangentes .
Compléter le tableau, sans justifier ( c'est-
à-dire uniquement par lecture graphique en
utilisant les points indiqués sur la figure ) .
x
(
)
'
f x
Equation de la tangente
au point d’abscisse
x
0
1
2

2
Exercice 4:
f
est la fonction définie sur par
2
3
( )
1
x
f x
x
=
+
.
1. Démontrer que
f
est dérivable sur et calculer
'( )
f x
.
2. Déterminer l’équation de la tangente
∆
à
f
C
au point d’abscisse a=1.
3. Etudier la position de
f
C
par rapport à la tangente
∆
.
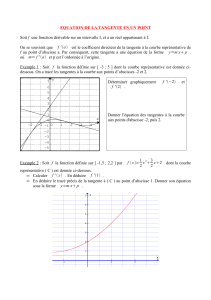
Exercice 5:
A l’aide d’une calculatrice, on a obtenu une partie de la courbe représentative de la fonction
f
définie
sur par
4 2
3
( ) 8
4 2
x x
f x x
= + + +
.
1. En combien de points la courbe semble-t-elle avoir une tangente parallèle à l’axe des abscisses ?
2. Trouver la valeur exacte des abscisses de ces points par le calcul ( on pourra factoriser par
x
).
Exercice 6:
f
est la fonction définie sur
+
par ( )
f x x
= .
1. Vérifier que, pour
0
h
>
,
(1 ) (1) 1
1 1
f h f
hh
+ −
=
+ +
.
2. En déduire l’existence et la valeur de
'(1)
f
.
Exercice 7:
f
est la fonction définie sur par
2
( )
f x x
=
et a est un nombre réel.
1. Donner l’approximation affine locale de
( )
f a h
+
.
2. Déterminer, en fonction de h, l’erreur commise lorsque l’on remplace
( )
f a h
+
par cette approximation
affine locale.
3. Comment choisir
h
pour que la précision de cette approximation soit égale à 10
-6
?

3

4

5