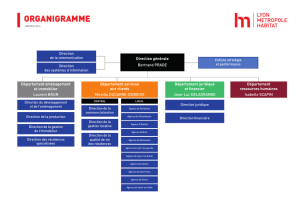
cours - MathsFG

Nombre d´eriv´e - cours - 1eSTG
F.Gaudon
27 mai 2008
Table des mati`eres
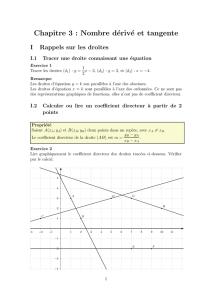
1 Tangente `a une courbe 2
2 Nombres d´eriv´es de fonctions usuelles 4
2.1 Nombres d´eriv´es pour les fonctions usuelles ........... 4
2.2 Op´erations sur les nombres d´eriv´es ............... 4
2.2.1 Somme ........................... 4
2.2.2 Multiplication par un nombre r´eel k........... 5
3 Signe d’un nombre d´eriv´e 5
1

1 Tangente `a une courbe
D´efinition :
On appelle tangente `a une courbe en un point Ade cette courbe, la droite
qui ”approche le mieux” la courbe en ce point.
D´efinition :
Soit Cla courbe repr´esentative d’une fonction fdans un rep`ere (O;~ i;~ j) et
soit Ale point de Cd’abscisse xA. Si la courbe admet au point d’abscisse
xAune tangente non parall`ele `a l’axe des ordonn´ees, alors le coefficient
directeur de cette tangente est appel´e nombre d´eriv´e de fen xAet not´e
f0(xA) (lire ”fprime de xindice A”).
2

Propri´et´e :
La tangente en un point Ad’abscisse xA`a la courbe repr´esentative de la
fonction fa pour ´equation ´equation r´eduite y=f0(xA)x+po`u f0(xA)
est le nombre d´eriv´e de fen xAet pest un r´eel `a d´eterminer.
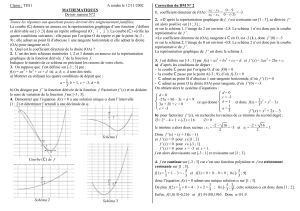
Exemple :
Soit fd´efinie par f(x) = x2pour tout xr´eel. On admet que f0(2) = 4 (voir
figure ci-dessus pour une visualisation et voir le paragraphe suivant pour
une justification). La tangente au point d’abscisse 2 a donc pour ´equation
y= 4x+po`u pest un r´eel. Or f(2) = 4 donc le point Ade coordonn´ees
(2; 4) appartient `a la tangente et on a 4 = 4 ×2 + pdonc p=−4. La
tangente au point d’abscisse 2 a donc pour ´equation y= 2x−4.
3

2 Nombres d´eriv´es de fonctions usuelles
2.1 Nombres d´eriv´es pour les fonctions usuelles
f(x)f0(x)
kconstant 0
x1
ax +b a
x22x
x33x2
1
x−1 x2
√x1
2√x
Exemple :
Soit fla fonction d´efinie pour tout r´eel xpar f(x) = x2. On a donc
f0(x) = 2xet en particulier f0(2) = 2 ×2 = 4 ce qui justifie le trac´e de la
tangente du paragraphe pr´ec´edent.
2.2 Op´erations sur les nombres d´eriv´es
2.2.1 Somme
Propri´et´e :
Soient uet vdeux fonctions d´efinies sur un intervalle Iet admettant un
nombre d´eriv´e en xA, alors u+vest d´efinie sur Iet admet un nombre
d´eriv´e en xAtel que :
(u+v)0(xA) = u0(xA) + v0(xA)
Exemple :
Soit ula fonction d´efinie sur R−{0}par u(x) = x3+1
x. Alors uadmet en
tout r´eel non nul xAun nombre d´eriv´e u0(xA) et on a u0(xA) = 3x2−1
x2.
Exemple
4

2.2.2 Multiplication par un nombre r´eel k
Propri´et´e :
Soient uune fonction d´efinie un intervalle Iet admettant un nombre
d´eriv´e en xA. Soit kun nombre r´eel, alors : ku est d´efinie sur I, admet
un nombre d´eriv´e en xAet :
(ku)0(xA) = ku0(xA)
Exemple :
Soit ula fonction d´efinie sur Rpar u(x) = 4x2. Alors la fonction uadmet
en tout r´eel xAun nombre d´eriv´e u0(xA) et on a u0(xA) = 4 ×2x= 8x.
3 Signe d’un nombre d´eriv´e
Propri´et´e :
– Si fest une fonction croissante sur un intervalle I, alors pour tout r´eel
xappartenant `a I, le nombre d´eriv´e f0(x) est positif.
– Si fest une fonction d´ecroissante sur un intervalle I, alors pour tout
r´eel xappartenant `a I, le nombre d´eriv´e f0(x) est n´egatif.
5