equations du second degre

Résolution d’équations du second degré
1) Equations du second degré
Définition
a, b, et c désignent des nombres réels donnés avec a ≠
≠≠
≠ 0.
Une équation du second degré, d’inconnue x, est une équation qui peut s’écrire sous la
forme 2
0
ax bx c
+ + =
.
Exemples
Après avoir factorisé, résoudre dans r, les équations suivantes :
a) 2
2 0
x x
− =
; b) 2
2 1 0
x x
+ + =
; c) 2
4 4 0
x x
− + =
; d) 2
9 0
x
− =
.
Solutions
a)
(
)
2
2 0 2 0 0 ou 2 0 0 ou 2
x x x x x x x x
− = ⇔ − = ⇔ = − = ⇔ = =
.
D’où S = {0 ; 2} : ensemble des solutions.
b)
( )
2
2
2 1 0 1 0 1 0 1
x x x x x
+ + = ⇔ + = ⇔ + = ⇔ = −
.
D’où S = {1} : ensemble des solutions.
c)
( )
2
2
4 4 0 2 0 2 0 2
x x x x x
− + = ⇔ − = ⇔ − = ⇔ =
.
D’où S = {2} : ensemble des solutions.
d)
(
)
(
)
2
9 0 3 3 0 3 0 ou 3 0 3ou 3
x x x x x x x
− = ⇔ + − = ⇔ + = − = ⇔ = − =
.
D’où S = {– 3 ; 3} : ensemble des solutions.
2) Fonction trinôme
a) Définition
Toute fonction polynôme du second degré est appelée fonction trinôme ; c’est-à-dire : toute
fonction définie sur r
rr
r du type :
(
)
2
f x ax bx c
= + +
avec a ≠
≠≠
≠ 0.
Exemples
1)
(
)
2
f x x
=
; ici a = 1, b = 0 et c = 0.
2)
( )
2
1
4
2
f x x x
= − + +
; ici
1
2
a
= −
, b = 1 et c = 4.
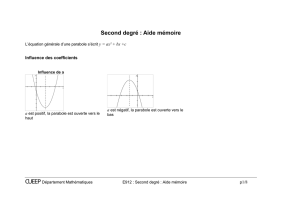
b) Représentation graphique
La représentation graphique d’une fonction trinôme, dans un repère orthogonal, est une parabole.
Exemple. Voir activité et chapitre 5
3) Racines du trinôme
a) Définition
On appelle racine du trinôme
(
)
2
f x ax bx c
= + +
(avec a ≠
≠≠
≠ 0) toute solution , quand elle
existe, de l’équation : 2
0
ax bx c
+ + =
.
Exemple.
(
)
2
4
f x x x
= +
(
)
( )
2
2
4 4
4 0 4 0 0ou 4 0 0 ou 4
x x x x
x x x x x x x x
+ = +
+ = ⇔ + = ⇔ = + = ⇔ = = −
On dit que –4 et 0 sont les racines de f.

b) Forme canonique - Discriminant
Exemple
(
)
2
2 7 6
f x x x
= + +
On met 2 en facteur
( )
2
7 6
2
2 2
f x x x = + +
2 2
2
2
2
7 7 7
2
4 4 4
7 7 49
4 2 16
x x x
x x x
+ = + × +
+ = + +
d’où
2
2
7 7 49
2 4 16
x x x + = + −
( )
( )
2
2
2
2
forme canonique
7 49 6
24 16 2
7 49 8 6
2
4 16 8 2
7 49 48
2
4 16 16
7 1
24 16
f x x
x
x
f x x
= + − +
×
= + − +
  ×
= + − −
= + −
(
)
2
f x ax bx c
= + +
(avec a ≠ 0)
On met a en facteur
( )
2
b c
f x a x x
a a
= + +
2 2
2
22
2
2
2
2 2 2
2 4
b b b
x x x
a a a
b b b
x x x
a a a
+ = + × +
+ = + +
d’où
2
2
2
2
2 4
b b b
x x x
a a a
+ = + −
( )
( )
22
2
22
2
22
2 2
22
2
forme canonique
2 4
4
2 4 4
4
2 4 4
4
2 4
b b c
f x a x a a a
b b a c
a x
a a a a
b b ac
a x a a a
b b ac
f x a x a a
= + − +
×
= + − +
×
= + − −
−
= + −
On a bien 2 2 2
4 7 4 2 6 1et 4 16
b ac a
− = − × × = =
c) Définition
On appelle discriminant du trinôme 2
ax bx c
+ +
(avec a ≠
≠≠
≠ 0) le réel 2
4
b ac
−, noté ∆
∆∆
∆.
Soit ∆
∆∆
∆ = 2
4
b ac
−.
∆ est appelé discriminant car il sert à discriminer (à distinguer) le nombre de solutions
(selon son signe).
La forme canonique du trinôme 2
ax bx c
+ +
(avec a ≠ 0) s’écrit alors :
( )
2
2
2 4
b
f x a x
a a
∆
= + − ; avec a ≠ 0.
Comme avec a ≠ 0, alors :
( )
2
2
0équivaut à 0
2 4
b
f x x a a
∆
= + − =
  .

4) Factorisation du trinôme
(
)
2
f x ax bx c
= + +
(avec a ≠
≠≠
≠ 0)
Résolution de l’équation du second degré 2
0
ax bx c
+ + =
(avec a ≠
≠≠
≠ 0).
Théorème
Soit une fonction trinôme f définie sur r
rr
r par :
(
)
2
f x ax bx c
= + +
; avec a ≠
≠≠
≠ 0
et ∆
∆∆
∆ = 2
4
b ac
−, son discriminant.
a) Si ∆
∆∆
∆ > 0, alors l’équation 2
0
ax bx c
+ + =
admet deux solutions distinctes :
1 2
et
2 2
b b
x x
a a
− + ∆ − − ∆
= =
et
(
)
(
)
(
)
1 2
f x a x x x x
= − − , factorisation de f(x).
Démonstration.
D’après c) :
( )
2
2
2 4
b
f x a x
a a
∆
= + − ; avec a ≠ 0.
(
)
( )
2
2
2
2
4 2
2
a a
a
∆
∆ ∆
= =
et
(
)
2
f x ax bx c
= + +
.
Donc
1 2
2
2
2
2 2 2 2 2 2
2 2 2 2 2 2
x x
b b b
ax bx c a x a x x
a a a a a a
b b b b
a x x a x x
a a a a a a
∆ ∆ ∆
+ + = + − = + − + + =
− ∆ − ∆ − + ∆ − − ∆
= − + − − = − −
Posons 1
2
b
x
a
− + ∆
= et 2
2
b
x
a
− − ∆
=. Ainsi
(
)
(
)
2
1 2
ax bx c a x x x x
+ + = − − : factorisation
et 2
0 ( 0) équivaut à
ax bx c a+ + = ≠
(
)
(
)
1 2 1 2 1 2
0 0ou 0 ou
a x x x x x x x x x x x x
− − = ⇔ − = − = ⇔ = =
.
Donc l’équation 2
0( 0)
ax bx c a
+ + = ≠
admet deux solutions distinctes :
1
2
b
x
a
− + ∆
= et 2
2
b
x
a
− − ∆
=.
Exemple
(
)
2
2 3
f x x x
= + −
. Ici a = 1, b = 2 et c = –3.
(
)
2 2
4 2 4 1 3 4 12 16
b ac
− = − × × − = + =
.
∆ > 0. L’équation 2
2 3 0
x x
+ − =
admet deux solutions distinctes :
1
2 16 2 4 2
1
2 2 1 2 2
b
x
a
− + ∆ − + − +
= = = = =
×
2
2 16 2 4 6
3
2 2 1 2 2
b
x
a
− − ∆ − − − − −
= = = = = −
×.
– 3 et 1 sont les racines du trinôme
(
)
2
2 3
f x x x
= + −
.
On peut factoriser :
(
)
(
)
(
)
1 2
f x a x x x x
= − − , soit
(
)
(
)
(
)
(
)
(
)
2
2 3 1. 1 3 1 3
x x x x x x
+ − = − − − = − +
. Donc
(
)
(
)
2
2 3 1 3
x x x x
+ − = − +
.

Interprétation graphique
( ) ( )
2
2 2
2 3 2 1 1 3 1 4
f x x x x x x
= + − = + + − − = + −
.
( ) ( )
2
1 4
f x x
= + −
.
La parabole d’équation 2
2 3
y x x
= + −
coupe l’axe des abscisses en deux points
d’abscisses respectives x1 = 1 et x2 = – 3.
b) Si ∆
∆∆
∆ = 0, alors l’équation 2
0
ax bx c
+ + =
admet une solution double : 0
2
b
x
a
= −
et
( ) ( )
2
0
f x a x x
= − , factorisation de f(x).
Démonstration.
0
2
2
2
Pour ( 0): 2 2
x
b b
a ax bx c a x a x
a a
≠ + + = + = − −
Posons 0
2
b
x
a
= − ; donc
( )
2
2
0
ax bx c a x x
+ + = − .
( ) ( )
2 2
2
0 0 0 0
0 0 0 0
ax bx c a x x x x x x x x
+ + = ⇔ − = ⇔ − = ⇔ − = ⇔ =
.
Donc l’équation 2
0
ax bx c
+ + =
( a ≠ 0 ) a une seule solution 0
2
b
x
a
= − .
Remarque :
(
)
(
)
(
)
( ) ( ) ( )
2
0 0 0
2
0 0 0
0 0
x x x x x x
x x x x x x
− = − −
− = ⇔ − − =
C’est pour cela que l’on dit que l’équation admet une solution double x0.
Exemple
( ) ( )
2
0
f x a x x
= − . Ici a = –1, b = 4 et c = –4.
(
)
(
)
2 2
4 4 4 1 4 16 16 0
b ac
− = − × − × − = − =
.
L’équation 2
4 4 0
x x
− + − =
admet une solution double :
( )
0
4 4
2
2 2 1 2
b
xa
= − = − = =
× −
et
( ) ( )
2
0
f x a x x
= − , soit alors
( )
2
2
4 4 1. 2
x x x− + − = − − . Donc
( ) ( )
2
2
f x x= − −
Remarque :
(
)
( )
2
2 2
4 4 4 4 2
x x x x x− + − = − − + = − − .

Interprétation graphique
La parabole d’équation 2
4 4
y x x
= − + −
a un seul point commun avec des
abscisses ; le point d’abscisse x0 = 2 .
c) Si ∆
∆∆
∆ < 0, alors l’équation 2
0
ax bx c
+ + =
n’admet pas de solution dans r
rr
r , on ne peut donc pas
factoriser f.
Démonstration.
( )
2
2
2 4
b
f x a x
a a
∆
= + − ; avec a ≠ 0.
2
4
a
∆
−> 0, et par suite
2
2
0
2 4
b
xa a
∆
+ + − >
    .
L’équation 2
0
ax bx c
+ + =
qui peut s’écrire
2
2
0
2 4
b
a x a a
∆
+ + − =
n’a pas de solution car a ≠ 0.
Exemple
(
)
2
2 2
f x x x
= − +
. Ici a = 1, b = –2 et c = 2.
( )
2
2
4 2 4 1 2 4 8 0
b ac
− = − − × × = − <
.
L’équation 2
0
ax bx c
+ + =
n’admet pas de solution réelle.
(
)
2
2 2
f x x x
= − +
n’est donc pas
factorisable dans r.
Interprétation graphique
La parabole d’équation 2
2 2
y x x
= − +
ne coupe pas l’axe des abscisses.
( ) ( )
2
2 2
2 2 2 1 1 2 1 1
f x x x x x x
= − + = − + − + = − +