Angles s Cours – trigonométrie Seconde

Secondes
Cours – trigonométrie
1
I.
a)
Le radian
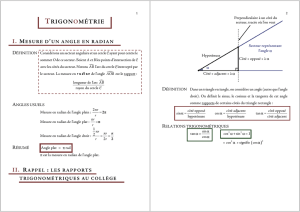
Définition : : C est le cercle de centre O et de rayon 1.
Le radian est la mesure de l’angle au centre qui intercepte sur C un arc de
longueur 1.
b)
Cercle trigonométrique
Angles dans un cercle
Définition : On appelle cercle trigonométrique un cercle orienté de rayon 1.
Orienté signifie "sur lequel on a choisi un sens". En l'occurence, le sens positif choisi, est le
sens inverse des aiguilles d'une montre.
~
ı
~
O1
1
−1
−1
La mesure en degré de 1 radian vaut
donc :
1 rd =180
π≃57˚
Remarque : Le radian est une grande
unité qui n’est pas intuitive contraire-
ment au degré qui est notre unité pre-
mière.
Avantage : Permet de connaître la lon-
gueur d’un arc. Unité du système inter-
national
Il est important de connaître les angles remarquables en radian :
Degré 30˚ 45˚ 60˚ 90˚
Radian π
6
π
4
π
3
π
2
+

2
Exemple : Convertir en radian les angles en degré suivants :
15˚ , 36˚ , 75˚ , 120˚ , 135˚ , 150˚
Pour convertir un angle en radian, on utilise la conversion 180˚=π rd, soit pour x
degré on a : xπ
180 radian.
On obtient alors :
Degré 15˚ 36˚ 75˚ 120˚ 135˚ 150˚
Radian π
12
π
5
5π
12
2π
3
3π
4
5π
6
Exemple : Convertir en degré les angles en radian suivant :
8,12 ,18 ,
π7π5π11π
6
Pour convertir un angle en degré, on utilise la conversion 180˚=πrd, soit pour y
π
y180
radian on a : degré.
Radian π
8
7π
12
5π
18
11π
6
Degré 22,5˚ 105˚ 50˚ 330˚
+ exercices concrets de la feuille projetée

3
II.
Cosinus et sinus d'un réel
Définition : L’abscisse du point M est le
cosinus du réel x, noté cos(x) ou
simplement cos x.
L’ordonnée du point M est le sinus du réel
x, noté sin(x) ou simplement sin x.
On obtient ainsi deux fonctions définies sur r :
Cos : x  cos(x) sin : x  sin(x)
Propriétés :
Pour tout réel x,
-1 ≤ cos(x) ≤ 1 -1 ≤ sin(x) ≤ 1 cos²(x) + sin²(x) = 1
Démonstration de cos²(x) + sin²(x) = 1
Le triangle OMC est rectangle en C.
En appliquant le théorème de Pythagore, on obtient : OM² = OC² + CM²
Soit cos²(x) + sin²(x) = 1 (car OM = 1)
Valeurs remarquables :
x 0 p
6
p
4
p
3
p
2p
cos x 1 3
2
2
2
1
20 -1
sin x 0 1
2
2
2
3
21 0
Soit x un nombre réel et M le point du cercle associé à x.
A tout réel x, on associe un point M du cercle trigonométrique par enroulement
de la droite des réels.
a)
b)Exemples : Si x = , ..... est le point
associé à . J a pour coordonnées ( ; )
J
I'
J'
I
p/2
p/2
donc cos = ..... et sin = .....
p/2 p/2
Exemples : Si x = , ..... est le point
associé à . I' a pour coordonnées ( ; )
p
p
donc cos = ..... et sin = .....
pp