Dénombrement

Chapitre 1 Dénombrement
I) Permutations
On dispose de trois cubes où sont inscrits les lettres de l’alphabet A, B et C.
Combien de « mots » de 3 lettres peut-on former ?
Et si on dispose de quatre cubes ?
Conclusion : Avec un ensemble (non ordonné) {a, b, c}de trois éléments, je peux former 3 ×2×1
listes (ordonnées), comme par exemple (a, b, c), (b, a, c), (c, b, a), etc.
Je peux donc permuter 3 cubes de 3 ×2×1 manières différentes.
Définition
Soit nun entier naturel non nul. Le nombre n×(n−1) × · · · × 2×1est appelé factorielle n.
On note n! = n×(n−1) × · · · × 2×1
Conventionnellement, 0! = 1.
D’après l’exemple, nous pouvons donc dire maintenant que
Théorème
Le nombre de permutations d’un ensemble contenant néléments est n!.
Exemples :
➔Dénombrer toutes les manières possibles de distribuer un jeu de 32 cartes ?
➔Combien y a-t-il d’anagrammes du mot ZOÉ ?
➔du mot ANA ?
Ainsi, la procédure suivante permet de calculer les factoriels avec maxima ou XCAS
maxima Xcas
factorial (200) factorial (200)
Avec un programme en récursif
python Xcas
def f(n):
if n<=1: return 1
else: return n*f(n-1)
facto(n):={
local res;
if ( n<=0 ) { res:=1}
else { res:=n*facto(n-1)}
retourne res
}
II) Combinaisons
On distribue 3 cartes d’un jeu de 32 cartes. Combien y a-t-il de mains (combinaisons) possibles ?
1

Définition
Soit net pdeux entiers naturels et Eun ensemble contenant néléments. Un sous-ensemble
de Econtenant péléments est appelé une combinaison de péléments de Eou encore une
p-combinaison d’éléments de E.
Exemple : Eest l’ensemble des cartes. n=CardE = 32. Une main possible est (7t, Dq, Ac) est
un sous ensemble de Econtenant p= 3 éléments.
C’est une combinaison de 3 éléments de E.
Définition
Le nombre de p-combinaisons d’un ensemble contenant néléments est noté n
p!ou encore Cp
n
Le nombre de mains possibles est donc noté 32
3!
Par exemple, on pourrait dire que j’ai 32 manières de choisir la première carte, 31 pour la deuxième
et 30 choix pour la troisième, donc il y a 32 ×31 ×30 façons d’avoir 3 cartes.
Par exemple (7t,Dq,Ac) mais dans une main l’ordre des cartes importe peu, la preuve on trie
généralement les cartes.
ainsi (7t, Dq, Ac) (7t, Ac, Dq) (Dq, 7t, Ac) (Dq, Ac, Dq) (Ac, 7t, Dq) (Ac, Dq, 7t) repré-
sente la même main.
il y a 3! façons d’ordonner ces nombres donc finalement :
5
3!=32 ×31 ×30
3!
On généralise la formule suivante :
Propriété
Pour tous entiers naturels net ptels que 0≤p≤n
n
p!=n(n−2)(n−3···(n−(p−1))
p!
Nous pouvons formuler cette propriété plus synthétiquement. En effet
n
p!=n(n−1)(n−2) ···(n−p+ 1)
p!×(n−p)(n−p−1)(n−p−2) × · · · × 2×1 (n−p)(n−p−1)(n−p−2) × · · · × 2×1=n! p!(n−p)!
d’où
Théorème
Pour tous entiers naturels net ptels que 0≤p≤n n
p!=n!
p!(n−p)!
TS Page 2

maxima Xcas
binomial (10,2) binomial (10,2) ou comb(10,2)
Remarque : Pour tous entiers naturels n, n
0!= n n!= 1 et n 1!= n n−1!=n
III) Triangle de Pascal - Binôme de Newton
À l’aide des formules précédentes, établissez que
Propriété
Pour tous entiers naturels net ptels que 0≤p≤n,
n
p!= n n−p!
Établissez, toujours par le calcul, la relation suivante, dite Relation de Pascal
Propriété
Pour tous entiers naturels net ptels que 0≤p≤n−1.
n
p!+ n p+ 1!= n+ 1 p+ 1!
Théorème
Soit aet bdes nombres complexes et nun entier naturel non nul, alors
(a+b)n=
n
X
p=0 n
p!apbn−p=an+ n 1!an−1b+···+ n n−1!abn−1+bn
On peut prouver cette formule par récurrence en remarquant que (a+b)k+1 =a(a+b)k+b(a+b)k
et en utilisant la relation de Pascal au bon moment.
Cette formule nous permet donc d’obtenir de nouveaux « produits remarquables », à conditions
de connaître les coefficients binomiaux.
Testez la formule aux rangs 2, 3, 4, 5. Disposez vos résultats dans un tableau en n’écrivant que
les coefficients et conjecturer le triangle de Pascal...
IV) ÉPREUVE DE BERNOULLI
TS Page 3

Définition
•On appelle épreuve de Bernoulli une épreuve ayant deux éventualités :
L’éventualité Sappelé succès avec la probabilité pet l’éventualité Sappelé échec avec la pro-
babilité 1−p.
•La loi de Bernoulli est la variable aléatoire Xtelle que X= 1 si le succès est réalisé et 0
sinon.
P(X= 1) = p,pest appelé paramètre de la loi de Bernoulli X.
La loi de probabilité de Xest xi1 0
p(X=xi)p 1-p
Propriété
Si Xsuit une loi de Bernoulli de paramètre palors E(X) = pet V(X) = p(1 −p).
Preuve : E(X) = 1 ×p+ 0 ∗(1 −p) = p
V(X) =
2
X
i=1
pix2
i−E(X)2=p×12+ (1 −p)×02−p2=p−p2=p(1 −p).
Exemple, La probabilité d’avoir un garçon est de 0,52, et donc d’avoir une fille de 0,48.
Avoir un enfant est donc une épreuve de Bernoulli de paramètre p= 0,52.
Soit Gl’évènement avoir un garçon.
xi1 0
p(X=xi) 0,52 0,48
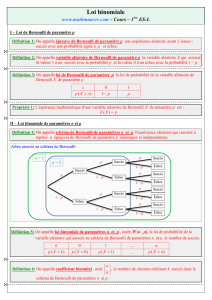
Imaginons maintenant que nous répétions cette expérience nfois.
Par exemple imaginons une famille de 4 enfants.
Définition
On répète nfois de façon indépendante une épreuve de Bernoulli de paramètre p.
Soit Xla variable aléatoire donnant le nombre de fois où le succès est réalisé. Alors Xsuit une
loi binomiale de paramètre net p.
On note cette loi B(n, p)
Exemple : X(Ω) = {0,1,2,3,4}
xi01234
p(X=xi)
Théorème
Soit Xune variable aléatoire suivant la loi binomiale B(n, p)et soit k∈ {0,1,2, ..., n}. Alors :
➔p(X=k) = n
k!pk(1 −p)n−k
➔on admettra que E(X) = np.
TS Page 4