Fiche 3 . 3 Etude d`une fonction homographique On

Fiche 3 . 3 Etude d’une fonction homographique
On considère une fonction homographique fde la forme x7−→ 2x+a
b−xoù aet bsont des réels.
−→ a et b sont inconnus et seront déterminés à la question 1.
1. Déterminer les réels aet bpour que la courbe représentative Cfde la fonction fpasse par les points A(3;−1) et Bµ5
2;0¶.
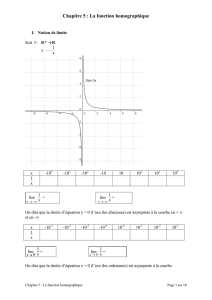
2. Dresser le tableau de variation de fsur l’intervalle I=]2;+∞[.
3. (a) Montrer que pour tout x6= 0,on a : f(x)=2−5
x
2
x−1.
(b) En déduire la limite de fen +∞
(c) Comment interpréter graphiquement cette limite ?
4. Montrer que la courbe Cfadmet une asymptote verticale et préciser son équation.
5. Compléter le tableau de variation de fen y ajoutant les limites de faux bornes de son ensemble de définition.
6. Déterminer le coefficient directeur de la tangente Tà la courbe de fau point B.
7. Etudier la position relative de Cfet de la droite Dd’équation y=x.
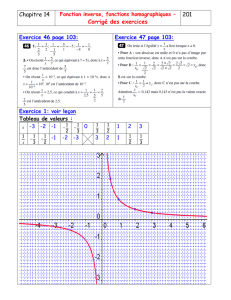
8. On donne la courbe de fen annexe. Construire les droites Tet Ddans le même repère.
Fiche 3 . 3 Etude d’une fonction homographique
On considère une fonction homographique fde la forme x7−→ 2x+a
b−xoù aet bsont des réels.
−→ a et b sont inconnus et seront déterminés à la question 1.
1. Déterminer les réels aet bpour que la courbe représentative Cfde la fonction fpasse par les points A(3;−1) et Bµ5
2;0¶.
2. Dresser le tableau de variation de fsur l’intervalle I=]2;+∞[.
3. (a) Montrer que pour tout x6= 0,on a : f(x)=2−5
x
2
x−1.
(b) En déduire la limite de fen +∞
(c) Comment interpréter graphiquement cette limite ?
4. Montrer que la courbe Cfadmet une asymptote verticale et préciser son équation.
5. Compléter le tableau de variation de fen y ajoutant les limites de faux bornes de son ensemble de définition.
6. Déterminer le coefficient directeur de la tangente Tà la courbe de fau point B.
7. Etudier la position relative de Cfet de la droite Dd’équation y=x.
8. On donne la courbe de fen annexe. Construire les droites Tet Ddans le même repère.
Fiche 3 . 3 Etude d’une fonction homographique
On considère une fonction homographique fde la forme x7−→ 2x+a
b−xoù aet bsont des réels.
−→ a et b sont inconnus et seront déterminés à la question 1.
1. Déterminer les réels aet bpour que la courbe représentative Cfde la fonction fpasse par les points A(3;−1) et Bµ5
2;0¶.
2. Dresser le tableau de variation de fsur l’intervalle I=]2;+∞[.
3. (a) Montrer que pour tout x6= 0,on a : f(x)=2−5
x
2
x−1.
(b) En déduire la limite de fen +∞
(c) Comment interpréter graphiquement cette limite ?
4. Montrer que la courbe Cfadmet une asymptote verticale et préciser son équation.
5. Compléter le tableau de variation de fen y ajoutant les limites de faux bornes de son ensemble de définition.
6. Déterminer le coefficient directeur de la tangente Tà la courbe de fau point B.
7. Etudier la position relative de Cfet de la droite Dd’équation y=x.
8. On donne la courbe de fen annexe. Construire les droites Tet Ddans le même repère.

Annexe :