1 Fonction inverse - Page personnelle de Julien Chenal

Fonction inverse
Fonction homographique
Cours
Représenter graphiquement la fonction inverse et connaître ses variations.
Identifier l’ensemble de définition d’une fonction homographique.
Objectifs du chapitre
1 Fonction inverse
1.1 Définition et variations
La fonction inverse est la fonction fdéfinie sur R∗par f(x)=1
x
Définition
On dit que 0 est une valeur interdite de la fonction inverse.
Remarques importantes!!
La fonction inverse est :
•strictement décroissante sur ] − ∞;0[.
•strictement décroissante sur ]0;+∞[.
Théorème
Attention, on ne peut pas dire que la fonction inverse est strictement décroissante sur R∗.
Remarques importantes!!
Le tableau de variations de la fonction inverse est le suivant :
x−∞ 0+∞
1
x
Propriété
1

Dans un tableau de variations, les valeurs interdites sont symbolisées par une double barre
verticale.
Remarques importantes!!
1.2 Courbe représentative
Voir activité.
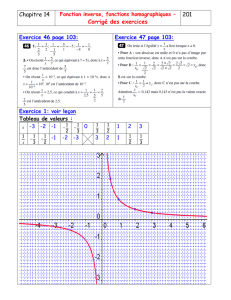
Tableau de valeurs :
x−2−1−0,5 −0,1 0 0,1 0,5 1 2 4
1
x−0,5 −1−2−10
@@
@@@
@
10 2 1 0,5 0,25
La fonction inverse est représentée
par une courbe H, appelée hyper-
bole.
Définition
Pour tout nombre xon a f(−x)=1
−x= − 1 x= − f(x). Les points M(x;f(x)) et M0(−x;f(−x))
sont donc symétriques par rapport à l’origine du repère.
Remarques importantes!!
2

2 Fonctions homographiques et signe d’une équation quotient
2.1 Etude d’un exemple
Une entreprise souhaite promouvoir une nouvelle sorte de céréales pour le petit-déjeuner.
L’entreprise estime qu’après xsemaines de publicité, le pourcentage de personnes
connaissant le nom de ces céréales est donné par p(x)=80x
x+1.
1) Calculer p(4). En déduire le pourcentage estimé de personnes ignorant le nom du pro-
duit après quatre semaines de publicité.
2) Avant la campagne de publicité, personne ne connait le nom de ces céréales. Vrai ou
Faux ? (Justifier)
3) Après 15 semaines de publicité, tout le monde connait le nom de cette céréale. Vrai ou
Faux ? (Justifier).
L’entreprise envisage une campagne de publicité de 10 semaines pour promouvoir ce
produit.
On s’intéresse donc à la fonction pdéfinie sur l’intervalle [0;10] par
p(x)=80x
x+1.
4) Compléter le tableau de valeurs suivant :
x0 1 2 3 4 5 6 7 8 9 10
p(x)
5) Tracer (Avec soin), sur [0;10], la représentation graphique de la fonction p.
6) Déterminer graphiquement la durée nécessaire pour que le pourcentage p(x) devienne
supérieur ou égal à 60 pour cent. (On laissera apparaitre les traits de construction)
7) Déterminer graphiquement combien de semaines supplémentaires de publicité sont
nécessaires pour que ce pourcentage dépasse 70 pour cent. (Traits de construction)
8) Le directeur de marketing de cette entreprise affirme que la campagne de publicité aura
un fort impact pendant les trois premières semaines, et qu’au-delà, ce sera beaucoup
plus limité. Cette affirmation vous semble-t-elle justifiée ? (Justifier)
Exercice
2.2 Fonction homographique
2.2.1 Définition
On appelle fonction homographique toute fonction fqui peut s’écrire sous la forme :
f(x)=ax +b
cx +d, où a,b,c,d∈Ret c6= 0.
Définition
3

2.2.2 Ensemble de définition
Une fonction homographique est définie pour tout xn’annulant pas son dénominateur.
Propriété
Déterminer l’ensemble de définition des fonctions suivantes :
1) f(x)=1
x−3.
2) g(x)=3x−2
2x−7.
3) h(x)=1
−5x+10.
Exercice
2.3 Signe d’une équation quotient
Déterminer le signe des équations suivantes :
1) x−4
x+6
2) 2x+4
3x−6
3) −2x+8
3x+9
Exercice
Résoudre les inéquations suivantes :
1) x+15
−8x+5≤0
2) 6x−3
x≥0
3) −9x+4
−x+7>0
Exercice
4