Fonction homographique

Seconde
Fonction homographique
1 D´efinition et propri´et´e
D´efinition :
On appelle fonction homographique f, une fonction qui au nombre xdiff´erent de −d
c, associe
le nombre ax +b
cx +d, o`u aet bsont deux nombres non tous les deux nuls et cun nombre non nul
et dun nombre.
f:x7→ f(x) = ax +b
cx +d.
Exercice :
Soit la fonction homographique ftelle que f(x) = 3x−2
7x+ 14.
Trouver la valeur interdite pour xc’est `a dire celle qui annule le d´enominateur 7x+ 14.
Exercice :
Dire si les expressions suivantes sont des fonctions fonctions homographiques, dans le cas
d’une r´eponse affirmative, pr´eciser les valeurs de a,b,cet d:
1. f1:x7→ f1(x) = 2x+ 1
−3x+ 5 ;
2. f2:x7→ f2(x) = 1
x;
3. f3:x7→ f3(x) = 2x
6x−1;
4. f4:x7→ f4(x) = −2
4x+ 1 ;
5. f5:x7→ f5(x) = 2 −2x−9
x;
6. f6:x7→ f6(x) = 2x−1
2;
7. f7:x7→ f7(x) = x+1
x;
8. f8:x7→ f8(x) = x+1
3.
S.Mirbel page 1 / 4

Seconde
2 Repr´esentation graphique :
Exercice :
Soit la fonction homographique ftelle que f(x) = 2x+ 1
4x−6.
1. Trouver la valeur interdite pour x.
2. Compl´eter le tableau de valeurs suivants :
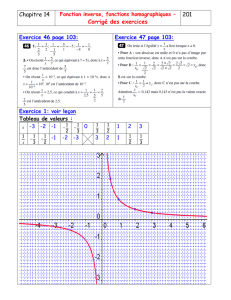
x-7 -6 -5 -4 -3 -2.5 -1.5 -1 0 1 2 3
f(x)
3. Repr´esenter la fonction fsur le graphique suivant :
−7−6.5−6−5.5−5−4.5−4−3.5−3−2.5−2−1.5−1−0.5 0.511.5 2 2.5 3
−2
−1.5
−1
−0.5
0.5
1
1.5
2
2.5
3
0
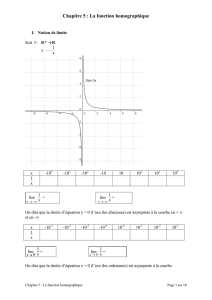
Th´eor`eme :
Une fonction homographique est repr´esent´ee par une hyperbole H, son centre de sym´etrie Ia
pour coordonn´ees −d
c;a c.
S.Mirbel page 2 / 4

Seconde
3´ Etude des variations d’une fonction homographique
Th´eor`eme :
Soit une fonction homographique f, telle que f(x) = ax +b
cx +d(cnon nul).
fpeut s’´ecrire sous la forme f(x) = k+h
cx+d, o`u ket hsont deux nombres non tous les deux
nuls.
D´emonstration :
R´eduire au mˆeme d´enominateur la forme k+h
cx +det identifier les nombres ket hen
fonction de a,b,cet d.
Exercice :
1. R´eduire au mˆeme d´enominateur et simplifier les expressions suivantes, identifier les
nombres k,h,a,bet c:
(a) f1(x) = −1 + 5
2x+ 1 ;
(b) f2(x) = 7 −4
3x+ 4.
2. Soit la fonction ftelle que pour tout nombre x,f(x)=7−1
x.
Montrer que pour tout nombre xnon nul, f(x) = 7x−1
x.
Th´eor`eme :
Soit fune fonction homographique telle que f(x) = k+h
cx +d.
On donne les tableaux de variations des fonctions homographiques fsuivant le signe de c.h
(le tableau indique aussi un exemple de repr´esentation graphique) :
c.h < 0c.h > 0
−d
c
k
I
−d
c
k
I
Indication de d´emonstration :
On utilise les variations de la fonction ”inverse”, et la d´efinition des variations d’une fonction.
S.Mirbel page 3 / 4

Seconde
Exercice :
´
Etudier les variations des fonctions suivantes, et v´erifier les variations sur votre calculatrice
avec une fenˆetre graphique adapt´ee (indiquer les param`etres de la fenˆetre utilis´ee) :
1. f(x) = 3 −2
3x+ 6 ;
2. g(x) = −7 + 5
2x−7.
4 Signe d’une fonction homographique
Exemple :
Soit fune fonction homographique telle que f(x) = ax +b
cx +d.
on cherche les valeurs x1et x2les solutions respectives des ´equations ax +b= 0 et cx +d= 0
Le signe de f(x) se d´etermine par un tableau de signe en indiquant une double barre pour la
valeur interdite : supposons f(x) = −2x+4
5x+6 .
x1= 2 et x2=−6
5
—f(x)<0 sur l’intervalle ] − ∞;−6
5[∪]2; ∞[
—f(x)>0 sur l’intervalle ]−6
5; 2[ ;
—f(x) = 0 dans l’ensemble {2}.
Exercice :
1. D´eterminer le tableau de signe de f(x) = x−3
x+ 5 ; V´erifier sur avec le graphique de la
calculatrice.
2. D´eterminer le tableau de signe de f(x) = −2x+ 5
3x−8; V´erifier sur avec le graphique de la
calculatrice.
3. D´eterminer le signe de f(x) = −2−−1,5
2x+ 5 ; V´erifier sur avec le graphique de la
calculatrice.
S.Mirbel page 4 / 4