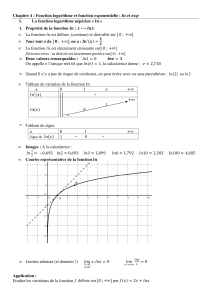
Soit f une fonction continue vérifiant pour tous réels x et y : { f(x) = 0 f

Terminale ES FONCTIONS EXPONENTIELLES Novembre 2015
DES FONCTIONS «TRANSFORMANT LES SOMMES EN PRODUITS »
Soit fune fonction continue vérifiant pour tous réels xet y:
f(x)6=0
f(x+y) = f(x)×f(y)
1. En écrivant que pour tout réel x,f(x) = fx
2+x 2, montrer que pour tout réel x,f(x)>0.
2. En écrivant que pour tout réel x,f(x+0) = f(x), calculer f(0)
3. Démontrer que pour tout réel x,f(−x) = 1
f(x)
4. On pose f(1) = q.
a) Calculer f(2)f(3)et f(0,5).
b) Calculer f(−1)et f(−2).
5. Démontrer que la suite (un)définie pour tout entier naturel npar un=f(n)est une suite géométrique.
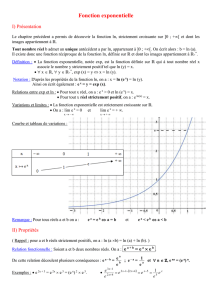
IFONCTIONS EXPONENTIELLES DE BASE q
1FONCTIONS EXPONENTIELLES x7−→ qx,AVEC q>0
Soit qun nombre strictement positif. La suite (un)définie pour tout entier npar un=qnest une suite géométrique
de raison q.
La fonction exponentielle de base qest le prolongement de cette suite géométrique.
DÉFINITION
Soit qun réel strictement positif
La fonction fdéfinie pour tout réel xpar f(x) = qxs’appelle la fonction exponentielle de base q.
On admet que cette fonction est dérivable sur R.
EXEMPLE
La fonction fdéfinie pour tout réel xpar f(x) = 0,8xest la fonction exponentielle de base 0,8.
Une valeur approchée de l’image de −5,3 est obtenue à la calculatrice en tapant la séquence : 0.8 ∧( - 5.3 ).
RELATION FONCTIONNELLE
La fonction exponentielle fde base q>0 transforme les sommes en produits. Pour tous réels xet y:
f(x+y) = f(x)×f(y)
Autrement dit, pour tous réels xet y:qx+y=qx×qy.
CONSÉQUENCES
— Pour tous réels xet y,q−x=1
qxet qx−y=qx qy.
En effet, qx−x=qx×q−xsoit 1 =qx×q−xdonc qx6=0 et q−x=1
qx.
De plus, qx−y=qx+(−y)=qx×q−y=qx
qy
D’APRÈS A. YALLOUZ (MATH@ES) Page 1 sur 4

Terminale ES FONCTIONS EXPONENTIELLES Novembre 2015
— Pour tout réel x,qx>0.
En effet, qx
2+x 2=qx 2×qx 2soit qx=qx 22avec qx6=0.
— Pour tout réel x,qx
2=√qx, et en particulier q0,5=√q
En effet, qx=qx
22et qx>0.
— Pour tout réel xet tout entier relatif m,(qx)m=qmx
Propriété usuelle des exposants entiers relatifs.
— Pour tout entier naturel n>0, q1
nest « la racine n-ième » de q
Pour tout entier naturel n>0, comme 1
n×n=1, alors q1
nest le nombre tel que q1 nn=q
2SENS DE VARIATION
En continuité avec les suites numériques, on admet que le sens de variation de la fonction exponentielle de base
qavec q>0 est le même que celui de la suite géométrique associée :
— Si 0 <q<1, la fonction x7−→ qxest strictement décroissante sur R.
— Si q=1, la fonction x7−→ qxest constante sur R.
— Si q>1, la fonction x7−→ qxest strictement croissante sur R.
CONSÉQUENCE
Si q>0 et q6=1, alors pour tous nombres réels aet b:qa=qbsi, et seulement si, a=b.
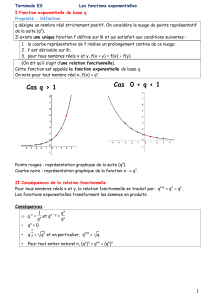
3PROPRIÉTÉS
0<q<1q>1
La fonction exponentielle de base qest strictement
décroissante sur R.
La fonction exponentielle de base qest strictement
croissante sur R.
lim
x→−∞
qx= +∞et lim
x→+∞
qx=0lim
x→−∞
qx=0 et lim
x→+∞
qx= +∞
1
1
0x
y
q1
1
0x
y
q
La fonction fonction exponentielle de base qest convexe sur R
D’APRÈS A. YALLOUZ (MATH@ES) Page 2 sur 4

Terminale ES FONCTIONS EXPONENTIELLES Novembre 2015
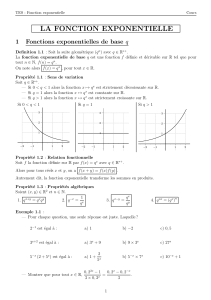
II LA FONCTION EXPONENTIELLE
On admet que parmi toutes les fonctions exponentielles de
base qil existe une seule fonction dont le nombre dérivé
en 0 soit égal à 1. ( cf. exercice no2 page 39 fait avec
geogebra)
Autrement dit, il existe une seule valeur du réel qtelle que
la tangente au point A(0;1)de la courbe représentative de
la fonction x7−→ qxa pour coefficient directeur 1.
Cette valeur particulière du réel qest notée e.
Le nombre e est un irrationnel une valeur approchée est :
e≈2,71828.
1
2
3
4
-1
1 2 3-1-2-3 0x
yy=ex
y=x+1
e
A
1DÉFINITION
La fonction x7−→ exs’appelle la fonction exponentielle de base e ou plus simplement exponentielle.
On la note exp
exp : x7−→ ex
CONSÉQUENCES
— La fonction exponentielle est définie pour tout réel xpar exp(x) = ex
— exp(0) = e0=1, exp(1) = e1=e, exp(−1) = e−1=1
e, exp(0,5) = e0,5=√e
— La fonction exponentielle est strictement positive sur R: pour tout nombre réel x, ex>0
— La fonction exponentielle est dérivable sur Ret son nombre dérivé en 0 est 1 : exp′(0) = 1
— Pour tous réels xet y, et pour tout entier relatif m
ex+y=ex×ey, e−x=1
ex, ex−y=ex ey,(ex)m=emx
2DÉRIVÉE DE LA FONCTION EXPONENTIELLE
La dérivée de la fonction exponentielle est la fonction exponentielle. Pour tout nombre réel x,
exp′(x) = ex
PREUVE
Pour tout réel xet pour tout réel h6=0,
exp(x+h)−exp(x)
h=ex+h−ex h=ex×eh−ex h=ex×eh−1 h
Or exp′(0) = 1 signifie que lim
h→0
e0+h−e0
h=1 soit lim
h→0
eh−1
h=1.
Donc pour tout réel x, lim
h→0
exp(x+h)−exp(x)
h=lim
h→0ex×eh−1
h=ex
3VARIATION
La fonction exponentielle est strictement croissante sur R
D’APRÈS A. YALLOUZ (MATH@ES) Page 3 sur 4

Terminale ES FONCTIONS EXPONENTIELLES Novembre 2015
PREUVE
La fonction exponentielle est dérivable sur Ret est égale à sa dérivée.
Or pour tout réel x, ex>0. On en déduit que la fonction exponentielle est strictement croissante sur R.
CONSÉQUENCES
— Pour tout réel x60, 0 <ex61
— Pour tout réel x>0, ex>1
— Pour tous réels xet y, ex=ey⇐⇒ x=yet ex<ey⇐⇒ x<y
III EXPONENTIELLE D’UNE FONCTION :exp(u)
On considère une fonction udéfinie sur un intervalle I.
La composée de la fonction usuivie de la fonction exponentielle est la fonction fnotée f=eu.
EXEMPLE
La fonction fdéfinie pour tout réel xpar f(x) = e0,5x−3est la composée de la fonction affine udéfinie sur R
par u(x) = 0,5x−3 suivie de la fonction exponentielle, f=eu.
1DÉRIVÉE
Soit uune fonction définie et dérivable sur un intervalle I. La fonction euest dérivable sur Iet
(eu)′=eu×u′
EXEMPLES
1. Soit fla fonction définie pour tout réel xpar f(x) = e−x.
Pour tout réel x, on pose u(x) = −x.uest dérivable sur Ret u′(x) = −1.
Donc fest dérivable sur Ret f′(x) = −e−x.
Or e−x>0 sur Rdonc f′(x)<0 sur Ret fest strictement décroissante sur R
2. Soit fla fonction définie pour tout réel xpar f(x) = e0,5x2−2x+1.
Pour tout réel x, posons u(x) = 0,5x2−2x+1. uest dérivable sur Ret u′(x) = x−2.
Donc fest dérivable sur Ret f′(x) = (x−2)e0,5x2−2x+1.
Or e0,5x2−2x+1>0 sur Rdonc f′(x)est du signe de (x−2)sur R.
Donc fest strictement décroissante sur ]−∞; 2[puis strictement croissante sur ]2 ; +∞[.
2VARIATION
Les fonctions uet euont les mêmes variations sur tout intervalle Ioù uest définie.
PREUVE
Si uest dérivable sur I, alors la fonction f=euest dérivable sur Iet pour tout réel x∈I,f′(x) = u′(x)eu(x).
Or pour tout réel x∈I, eu(x)>0 donc f′(x)est du même signe que u′(x).
EXEMPLE
La fonction fdéfinie pour tout réel xpar f(x) = e0,5x−3a les mêmes variations que la fonction affine udéfinie
sur Rpar u(x) = 0,5x−3.
Donc fest strictement croissante sur R.
D’APRÈS A. YALLOUZ (MATH@ES) Page 4 sur 4