Cours condense TES fonctions exponentielles

Terminale ES Les fonctions exponentielles
1
I Fonction exponentielle de base q
Propriété - Définition
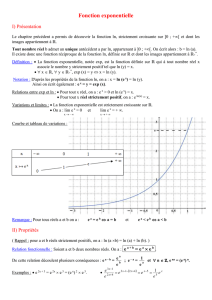
q désigne un nombre réel strictement positif. On considère le nuage de points représentatif
de la suite (q
n
).
Il existe une unique fonction f définie sur  et qui satisfait aux conditions suivantes :
1. la courbe représentative de f réalise un prolongement continu de ce nuage;
2. f est dérivable sur ;
3. pour tous nombres réels x et y, f(x + y) = f(x) × f(y)
(On dit qu’il s’agit d’une relation fonctionnelle).
Cette fonction est appelée la fonction exponentielle de base q.
On note pour tout nombre réel x, f(x) = q
x
.
Points rouges : représentation graphique de la suite (q
n
).
Courbe noire : représentation graphique de la fonction x → q
x
.
II Conséquences de la relation fonctionnelle
Pour tous nombres réels x et y, la relation fonctionnelle se traduit par : q
x+y
= q
x
× q
y
.
Les fonctions exponentielles transforment les sommes en produits.
Conséquences :
• q
-x
= 1
q
x
et q
x – y
= q
x
q
y
• q
x
> 0.
• q
x
2
= q
x
et en particulier, q
0,5
= q
• Pour tout entier naturel n, (q
x
)
n
= q
nx
= (q
n
)
x
Cas q > 1
Cas 0 < q < 1

Terminale ES Les fonctions exponentielles
2
III Sens de variation
Propriétés
Le sens de variation de la fonction x → q
x
est le même que celui de la suite géométrique
associée.
• Si 0 < q < 1, la fonction x → q
x
est strictement décroissante sur .
• Si q = 1, la fonction x → q
x
est constante sur .
• Si q > 1, la fonction x → q
x
est strictement croissante sur .
IV La fonction exponentielle x  e
x
Propriété - Définition
Il existe une unique fonction x → q
x
qui admet pour nombre dérivé 1 en 0.
On note e la base de cette fonction exponentielle et e ≈ 2,718.
On dit que la fonction exponentielle de base e est la fonction exponentielle.
Elle se note exp : x → e
x
.
Conséquences :
• La fonction exponentielle est dérivable sur  et exp’(0) = 1.
• exp(0) = e
0
= 1 exp(1) = e
1
= e exp(-1) = e
-1
= 1
e exp(0,5) = e
0,5
= e
• Pour tout réel x, e
x
> 0.
• La fonction exponentielle est strictement croissante sur  (car e > 1).
On en déduit que pour tous réels a et b :
e
a
= e
b
⇔ a = b e
a
< e
b
⇔ a < b
Conséquence
:
Si q ≠ 1, alors pour tous nombres réels
a et b :
q
a
= q
b
⇔ a = b
exp
T
Tangente en A(0,1) de coefficient
directeur égal à 1

Terminale ES Les fonctions exponentielles
3
Propriétés algébriques :
Pour tous réels x et y et pour tout entier relatif n :
e
x+y
= e
x
×e
y
e
x
2
= e
x
e
-x
= 1
e
x
e
x – y
= e
x
e
y
(e
x
)
n
= e
nx
V Dérivée de la fonction exponentielle
Propriété
La fonction exponentielle est égale à sa fonction dérivée.
Ainsi, pour tout réel x, exp’(x) = e
x
.
VI Courbe représentative de la fonction exponentielle
VII Fonction dérivée de x  e
u(x)
Propriété
Si la fonction u est dérivable sur un intervalle I, alors la fonction x  e
u(x)
est dérivable
sur I et pour tout réel x de I : (e
u
)’(x) = u’(x) × e
u(x)
.
•
Tableau de variation de la fonction exponentielle :
• Equation de la tangente T
0
à 
exp
au point A(0,1) :
exp’(0) = 1 donc T
0
: y = 1(x – 0) + 1, soit y = x + 1
• Equation de la tangente T
1
à 
exp
au point B(1,e) :
exp’(1) = e donc T
1
: y = e(x – 1) + e, soit y = ex
x
f'
f(x)
-
∞
+
+
∞
0
1
1
e
exp
T
1
T
0
Conséquence
:
Les fonctions u et e
u
ont le même sens de variation sur l’intervalle I.
En effet, comme pour tout
réel x de I e
u(x)
> 0 alors
(e
u
)’(x) et u’(x) ont le même signe.

Terminale ES Les fonctions exponentielles
4
VIII Exemples types
Exemple 1 : les fonctions f
k
: x → e
-kx
avec k réel strictement positif.
Ces fonctions sont de la forme e
u
avec u(x) = - kx.
Elles sont donc dérivables sur  et pour tout x réel :
f‘
k
(x) = -ke
-kx
; donc f’
k
(x) < 0 : les fonctions f
k
(avec k > 0) sont strictement décroissantes
sur .
Exemple 2 : les fonctions g
k
: x → e
-kx²
avec k réel strictement positif.
Ces fonctions sont de la forme e
u
avec u(x) = - kx².
Elles sont donc dérivables sur  et pour tout x réel :
g‘
k
(x) = -2kxe
-kx²
; Or 2e
-kx²
> 0 donc g’
k
(x) a le même signe que –x.
les fonctions g
k
(avec k > 0) sont croissantes sur ]- ∞;0] et décroissantes sur [0;+ ∞[.