TES Jeudi 04 avril 2013 DEVOIR SURVEILLE N°6 EXERCICE 1 : 5

TES
Jeudi 04 avril 2013
DEVOIR SURVEILLE N°6
EXERCICE 1 : 5 points
Cet exercice est un questionnaire à choix multiples ; pour chacune des questions, une et une seule
réponse est exacte. Indiquez sur votre copie le numéro de la question et la bonne réponse sans
justifier votre choix.
Chaque bonne réponse rapporte 1 point et une mauvaise réponse enlève 0,5 point.
1. Soit la fonction f définie sur ℝ par xxxf 124
3
−=)( . La primitive de f qui s’annule en 1 est la
fonction F définie par :
a. 24 6xxxF −=)( b. 56
24
+−= xxxF )( c. 1212
2
−= xxF )(
2. La fonction f définie sur ℝ par x xxf e=)( a pour primitive la fonction F définie sur ℝ par :
a.
x
xxF
e
)()( 1+= b.
2
2x
x
xF
e
=)( c.
x
xxF
e
)()( 1−=
3.
∫
−
+
4
2
12
dx
x
e est égale à :
a. e9 – e-3 b. e9 – e-3
2 c. 2(e9 – e-3)
4. La valeur moyenne sur [- 1 ; 2] de la fonction f définie sur ℝ par
2
3xxf =)( est égale à :
a. 9 b. 3 c. 7
3
5. Soit une variable aléatoire qui suit la loi normale centrée réduite. P(X ≥─ 2), arrondie au
millième, est :
a. 0,977 b. 0,023 c. 0,477
EXERCICE 2: 3,5 points
Un étang de pêche est très régulièrement empoissonné. Lorsqu’un pécheur met sa ligne à l’eau, le
temps d’attente T en minutes avant la 1er touche suit la loi uniforme sur l’intervalle [0 ; 15]
1. Quelle est la probabilité pour que ce temps d’attente soit :
a. égal à 5 min
b. supérieur à 10 min
c. inférieur à 30 s.
2. Quel est le temps moyen d’attente ?
EXERCICE 3: 4 points
On considère la fonction f définie sur [ 0 ; 2] par :
f(x) = x si 0  x  1
2 – x si 1 < x  2
On donne la représentation graphique de la fonction f ci-contre
1. Montrer que f est une fonction de densité sur [0 ; 2].
2. Soit X la variable aléatoire de densité f .
Calculer P( 1  X  2) et P( 0,5  X  1,5)

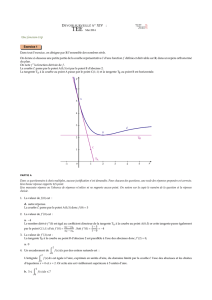
EXERCICE 4: 7 points
La courbe f
C
tracée ci- contre est la représentation
graphique d’une fonction f définie et dérivable sur ℝ .
On note la fonction dérivée de f .
La tangente T à la courbe
f
C
au point A(0 ; 3) passe par le
point B(1 ; 5).
1. En utilisant les données et le graphique :
a. Déterminer f(0) et f’(0).
b. Donner un encadrement par deux entiers
consécutifs de l’aire, en unités d’aire, de la partie du plan
située entre la courbe
f
C
, l’axe des abscisses, l’axe des ordonnées et la droite d’équation x = 1.
2. On admet que la fonction f est définie, pour tout nombre réel x , par une expression
de la forme  1  où et sont des nombres réels.
a. Déterminer l’expression de en fonction de , et x .
b. À l’aide des résultats de la question 1.a., démontrer que l’on a, pour tout réel x :  1 
3. Soit F la fonction définie et dérivable sur ℝ par
a. Vérifier que F est une primitive de f sur ℝ .
b. Déterminer la valeur exacte puis une valeur approchée à 10
−2
près de l’aire, en unités d’aire, de
la partie du plan située entre la courbe
f
C
, l’axe des abscisses, l’axe des ordonnées et la droite
d’équation x = 1.
Ce résultat est-il cohérent avec l’encadrement obtenu à la question 1b ?

CORRIGE DU DEVOIR SURVEILLE N°6
EXERCICE 1 :
1. 56
24
+−= xxxF )( 2. x xxF e)()( 1−= 3. e
9
– e
-3
2
4. 3 5. 0,977
EXERCICE 2: 3,5 points
1. a. P(T = 5) = 0
b. P(T ≥ 10) = P( 10  T  15) = 15 – 10
15 – 0 = 1 3
c. P(T < 0,5) = P ( 0  T  0,5) = 0,5 – 0
15 - 0 = 1 30
2. E(T) = 0 + 15
2 = 7,5 : le temps moyen d’attente est de 7 min 30 s.
EXERCICE 3: 3,5 points
On considère la fonction f définie sur [ 0 ; 2] par : f(x) = x si 0  x  1
2 – x si 1 < x  2
On donne la représentation graphique de la fonction f ci-contre
1.  Pour x = 1 f(1) = 1 et 2 – x = 2 – 1 = 1 donc f est continue sur [ 0 ; 2]
 Pour tout x ∈ [ 0 ; 1 ] x ≥ 0 et pour tout x ∈ [ 1 ; 2] , 2 – x ≥ 0 donc f est positive sur [ 0 ; 2]
 L’aire du domaine compris entre la courbe représentative de f et l’axe des abscisses sur [ 0 ; 2]
est l’aire du triangle de base 2 et de hauteur 1 soit 2 x 1
2 = 1 .
La fonction f est donc bien une fonction de densité sur [ 0 ; 2]
2. a. P( 1  X  2) =
∫
2
1
dxxf )(
=
∫
−
2
1
2dxx)(
= F(2) – F(1)
où F(x) =2x - x2
2
= 2 – 1,5 = 0,5
Ou bien :
P( 1  X  2) = 1 x 1
2
= 0,5
(aire du triangle rectangle)
b. P( 0,5  X  1,5) =
∫
51
50
,
,
)( dxxf
=
∫∫
−+
51
1
1
50
2
,
,
)( dxxxdx
= G(1) – G(0,5) + F(1,5) –
F(1)
où G(x) = x
2
2
= 0,5 – 0,125 + 1,875 – 1,5
= 0,75
Ou bien :
P( 0,5  X  1,5) = 1 – 0,5 x 0,5
2 x 2
= 0,75
( aire sous la courbe – aire des 2 « petits » triangle
rectangle)

EXERCICE 4:
1. a. f (0) = 3 car A(0 ; 3) appartient à la courbe f
C
f ’(0) est le coefficient directeur de la tangente f
C
au point d’abscisse 0, c'est-à-dire le
coefficient directeur de la droite T donc : f ’(0) = Y
B
– Y
A
x
B
- xA = 5 – 3 1 – 0 = 2
b. 3  Aire  4 car elle est comprise entre l’aire de deux rectangles de
largeur 1 et de longueur respective 3 et 4. et la droite d’équation x = 1.
2. a. )(
)(
)( xv
xu
xf +=1 avec axubaxxu =+= )(')(
donc
xx exvexv == )(')(
donc
)(
)(')()()('
)(' xv
xvxuxvxu
xf
2
−
=donc
xx
xx
e
baax
e
ebaxae
xf −+− =
+−
=
2
)(
)('
b.
x
e
b
ax
f(x)
+
+=1 donc bf += 10)( .
Or d’après la question 1.a 30 = )( f donc 1 + b = 3 d’où b = 2
x
e
b
a
ax
xf
−
+
−
=)(' donc baf −=)(' 0.
Or d’après la question 1. a 20 =)('f donc a – b = 2 soit a – 2 = 2 d’où a = 4
Ainsi on a bien :
x
x
xf
e
1
24
+
+=)(
3. )( )(
x)( xv xu xF += avec 464 −=−−= )(')( xuxxu
donc
xx
exvexv == )(')(
donc
)(
24
1
644
1
)64(4
1)('
2
xf e
x
e
xe
exe
xF
xx
x
xx
=
+
+=
++−
+=
−−−−
+=
Donc F est bien une primitive de fsur ℝ.
b.
∫
1
0
dxxf )( = F(1) – F(0) = 1 - 10
e - (- 6) = 7 – 10 e  3,3
Donc Aire = 7 – 10
e  3,3 ua
Ce qui est cohérent avec le résultat trouvé à la question 1.b puisque 3  7 – 10
e  4