Télécharger

DM
Soient a un réel de ] 1 ; + ∞ [, et la surface triangulaire S délimitée par : les
tangentes à la courbe de la fonction inverse aux points d’abscisse a et 1/a, et
l’axe des abscisses. Pour quelle valeur de a la surface S a-t-elle une aire de
1,92 dans un repère orthonormé ?
Indications : déterminez les coordonnées des sommets du triangle.
Réponse :
Soit M( x ; y ) un point quelconque de la tangente à la courbe de f au point A d’abscisse a, donc
représentatif de tous les points de la tangente.
yM – yA y – f(a)
coefficient directeur de la tangente = qui devient f ‘(a) =
xM – xA x – a
puis f ‘(a) ( x – a ) = y – f(a) puis y = f ‘(a) ( x – a ) + f(a) ou y = f ‘(a) x + f(a) – a f ‘(a)
1 - 1
f(x) = donc f ‘(x) =
x x²
- 1 1 - 1 1 1 - 1 2
Tangente en A d’abscisse a : y = ( x – a ) + = x + + = x +
a² a a² a a a² a
- 1 1 1
Tangente en B d’abscisse 1/a : y = ( x – ) + = – a² x + a + a = – a² x + 2a
1 ² a 1
a a
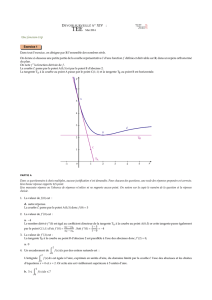
Exemple de tracé pour a ≈ 2
B
A
1/a 1 a

Intersections des tangentes avec l’axe des abscisses :
2 2
y = - a² x + 2a donne 0 = - a² x + 2a puis a² x = 2a puis x = donc le point ( ; 0 ).
a a
- 1 2 - 1 2 1 2
y = x + donne 0 = x + puis x = puis x = 2a donc le point ( 2a ; 0 ).
a² a a² a a² a
Intersections des tangentes entre elles : 2 2a² - 2
2a -
- 1 2 - 1 2 a a
y = x + = - a² x + 2a donne + a² x = 2a - puis x = =
a² a a² a - 1 - 1 + a4
+ a²
a² a²
2a² - 2 a² a 2a
donc x = × = 2 ( a² - 1 ) =
a a4 - 1 ( a² - 1 ) ( a² + 1 ) a² + 1
2a - 2a3 + 2a ( a² + 1 ) - 2a3 + 2a3 + 2a 2a
et y = - a² + 2a = = =
a² + 1 a² + 1 a² + 1 a² + 1
que l’on aurait aussi pu obtenir avec l’autre équation ( et qui peut servir de vérification facultative ).
2a 2a
Donc le point ( ; ).
a² + 1 a² + 1
Aire de la surface S : c’est un triangle donc ½ base × hauteur
Le seul couplet ( base ; hauteur ) déjà étudié est celui-ci :
2a/(a²+1) e
2a/(a²+1) 2/a 2a

2a 2
donc hauteur = et base = 2a –
a²+1 a
1 2 2a 2a² - 2 a 2a² - 2
Aire = 2a - = =
2 a a² + 1 a a² + 1 a² + 1
2a² - 2
Aire = 1,92 = 1,92 2a² - 2 = 1,92 ( a² + 1 ) 2a² - 2 = 1,92 a² + 1,92
a² + 1
2a² - 1,92 a² = 1,92 + 2 0,08 a² = 3,92
3,92 392 49 × 8
a² = = = = 49 a = 7 ou a = - 7
0,08 8 8
mais pas de solution a négative dans ] 1 ; + ∞ [.
Réponse : une unique solution a = 7 pour obtenir une aire de 1,92.