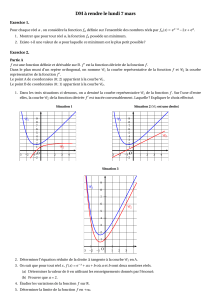
CALCUL INTEGRAL I. Généralités. 1) Théorème : Soit f une fonction

CALCUL INTEGRAL
I. Généralités.
1) Théorème :
Soit f une fonction dérivable sur I et a,b deux nombres appartenant à I.
Le nombre F(b)-F(a) où F est une primitive de f, ne dépend pas du choix de F.
preuve : Soient F et F+C , C un réel quelconque, deux primitives de f.
( F(b)+C ) -(F(a) + C) = F(b)-F(a)+C-C= F(b)-F(a)
2) Définition :
Soit f une fonction admettant F comme primitive sur I et a, b deux nombres de I.
Le nombre F(b)-F(a) s’appelle intégrale de a à b de f et se note
b
a
dx)x(f
on a
b
a
dx)x(f
= [F(x)]
b
a
= F(b)-F(a).
Exemples : a)
1
2
dt
²t
1
[
1
2
]
t1
= -1+
2
1
2
1
b)
4
3
dx
134]x[ 4
3
c)
e
1
dt
t
1
[lnt]
e
1
= 1
3) Interprétation graphique :
a) unité d’aire :
définition : Dans un repère orthogonal
)j,i;O( 
, soit I(1 ;0), J(0 ;1) et K(1 ;1).
On appelle unité d’aire et on note u.a l’aire du rectangle OIKJ.
exemple : Soit
)j,i;O( 
un repère orthogonal d’unités graphiques 2 cm en abscisse et
3 cm en ordonnées. L’unité d’aire est 6 cm². On écrit 1 u.a = 6 cm².
b) Activité :
On considère la fonction k définie sur  par k(x) = x-1
et représentée ci-contre. On cherche à déterminer
l'aire du domaine grisé sur le dessin ci-contre.
1. Calculer cette aire en cm2.
2. Trouver une primitive K de la fonction k
et calculer K(5)-K(1).
3. Que remarque-t-on ?
solution : 1. A =
²cm8
24x4 
2. Une primitive de k est K(x) =
x
2²x 
donc
81
2
1
5
2
25
)1(K)5(K 
3. On remarque que l’on trouve le même résultat.
c) Aire d’une partie de plan limitée par la courbe représentative d’une fonction f, l’axe Ox et
deux droites parallèles à l’axe Oy.
Soit f une fonction dérivable sur un intervalle [a ;b] et F une primitive de f .
 Cas d’une fonction ne prenant que des valeurs positives sur [a ;b]
Théorème admis :
Soit f une fonction dérivable sur [a ;b] et ne prenant que des valeurs
positives sur [a ;b]. Soit C la courbe représentative de f dans un repère
)j,i;O( 
. L’aire, exprimée en unités d’aire, de la partie de plan limitée
par C, l’axe Ox, la droite d’équation x = a et la droite d’équation
x = b est égale à
b
a
dx)x(f
2 3 4 5
2
3
4
0 1
1
x
y
a b
i
j
0 1
1
x
y
a b
i
j

 Cas d’une fonction ne prenant que des valeurs négatives sur [a ;b]
Théorème admis :
Soit f une fonction dérivable sur [a ;b] et ne prenant que des valeurs négatives sur [a ;b].
Soit C la courbe représentative de f dans un repère
)j,i;O( 
.
L’aire, exprimée en unités d’aire, de la partie de plan limitée par C, l’axe Ox,
la droite d’équation x = a et la droite d’équation x = b
est égale à
b
a
dx)x(f
En effet, A = A’=
b
a
dx)x(f
d’après le théorème précédent.
 Cas d’une fonction changeant de signe sur [a ;b]
Si f change de signe sur [a ;b], on calcule les aires sur chaque
sous-intervalle où f est de signe constant. L’aire totale est la somme des
aires calculées.
A =
c
a
dx)x(f
+
b
c
dx)x(f
ATTENTION : L’aire d’une partie de plan délimitée par la courbe représentative d’une fonction f, l’axe Ox,
la droite d’équation x = a et la droite d’équation x = b n’est pas toujours égale à
b
a
dx)x(f
exemple : 1) Calculer l’aire de la partie du plan délimitée par la courbe de la fonction f définie par
f(x) = x² - 1 , l’axe Ox, la droite d’équation x = -2 et la droite d’équation x = 3.
2) Calculer
3
2
dx)x(f
solution : 1) A =
1
2
dx)x(f
+
1
1
dx)x(f
+
3
1
dx)x(f
soit A =
1
2
dx)1²x(
+
1
1
dx)1²x(
+
3
1
dx)1²x(
A = [
3
x3
- x]
1
2
+ [ -
3
x3
+ x]
11
+ [
3
x3
- x]
3
1
=
3
28
)1
3
1
3
3
27
()1
3
1
1
31
()2
3)2(
1
31
(3
donc l’aire cherchée est
3
28
u.a.
2)
3
2
dx)x(f
= [
3
x3
- x]
32
= 9-3-(
)2
38
=
3
20
a b
i
j
C
C'
A'
A
0 1
1
x
y
a b
i
j
a b
i
j
c
0 1
1
x
y
a b
i
j
c
2 3 4 5-1-2
2
3
4
5
6
7
-1
0 1
1
x
y

4) Aire limitée par deux courbes :
Théorème : Soient f et g deux fonctions dérivables sur [a ;b] telles que pour tout x de [a ;b]
f(x) < g(x) et C et C’ leurs courbes représentatives respectives dans un repère
orthogonal
)j,i;O( 
.
L’aire de la partie du plan limitée par les courbes C et C’et par les droites
d’équation x = a et x = b est A =
b
a
dx))x(f)x(g(
(unités d’aire)
5) Valeur moyenne :
Définition : Soit f une fonction dérivable sur [a ; b]. On appelle valeur moyenne de f sur [a ; b]
le nombre réel
b
a
dx)x(f
ab1
Interprétation graphique :
Puisque
b
a
)ab(dx
, on a donc
b
a
b
a
dx)x(fdx
.
Ainsi, dans le cas d’une fonction positive sur [a ; b], l’aire du
domaine associé à une fonction f sur [a ; b] est égale à l’aire du
rectangle de dimensions  et b – a.
II. Propriétés :
Soient f et g deux fonctions ayant des primitives sur I et a,b et c appartenant à I.
1)
b
a
dx)x(f
= -
a
b
dx)x(f
2) Relation de Chasles :
b
a
dx)x(f
=
c
a
dx)x(f
+
b
c
dx)x(f
3) Soit k réel
b
a
dx)x)(kf(
= k
b
a
dx)x(f
4)
b
a
dx)x)(gf(
=
b
a
dx)x(f
+
b
a
dx)x(g
5) a et b sont deux réels tel que a < b, f et g deux fonctions dérivables sur [a ; b] de . Si pour tout réel x
de [a ; b]
b
a
b
a
dx)x(gdx)x(falors),x(g)x(f
. Donc si
0dx)x(falors,0)x(f b
a
.
6) Inégalité de la moyenne : soient m et M deux nombres réels
si m ≤ f ≤ M et si a ≤ b alors m(b-a) ≤
b
a
dx)x(f
≤ M(b-a).
D’après cette inégalité, f étant dérivable sur [a ; b], l’équation f(x) =  a au moins une solution dans [a ; b]. La
droite d’équation y =  coupe donc la courbe représentative de f en un point au moins. Si on considère les
parties de plan comprises entre cette droite, les droites d’équation x = a, x = b et le courbe représentant f,
l’aire située au dessus de la droite représentant la moyenne (y = ) est égale à l’aire située en dessous. (voir
figure ci-dessus).
Exercices p.150 n° 1, 2, 3, 4, 5, 6, 9, 10, 11, 13, 15, 16, 17, 18, 19, 21, 24, 25, 27, 29, 33, 34, 39, 41, 42, 44, 47
a b
i
j
C
C'
0 1
1
x
y
a b
i
j
i
j
a b
µ
2 3
2
0 1
1
x
y
i
j
a b
µ