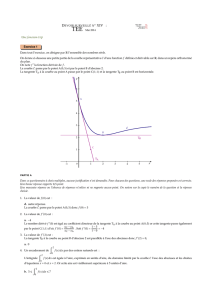
Modèle mathématique.

Introduction :
2
xx:f 
sur
1,0
.
D : le domaine plan limité par la courbe, l’axe des
abscisses et les droites d’équation
0x 
et
1x 
.
Calculons l’aire de D.
L’unité pour mesurer les aires est l’aire du rectangle
construit sur le repère
j,i,O
.
On subdivise
1,0
en n intervalles de même amplitude
n
1
.
n
s
est la somme des aires des « petits » rectangles situés sous la courbe.
Pour
2n 
Par ailleurs, pour
*
INp
61p21pp
p...321 2222 
.
Formule que l’on peut justifier par récurrence.
Donc
22
nn6
1n21n
n
1
61n21nn n
1
s
.
n
S
est la somme des aires des « grands » rectangles situés au dessus de la courbe.
Pour
2n 
Pour tout
2n 
nn SAs 
. A étant l’aire du domaine D.
On peut démontrer que
2n
n
s
est croissante.
On peut démontrer que
2n
n
S
est décroissante.
Pour
2n 
n
1
n6
1n21n
n6
1n21n
sS 22
nn 
0
n
1
limsSlim n
nn
n
.
Intégration
2
2
222
n
n
n
1n...321
n
1
s
n1n
f...
n
3
f
n
2
f
n
1
f
n
1
s
2
n
n
2
2222
n
n
n6
1n21n
S
61n21nn n
1
S
n
n...321
n
1
S
n
n
f...
n
3
f
n
2
f
n
1
f
n
1
S

Les suites
2n
n
s
et
2n
n
S
sont donc adjacentes, elles convergent vers la même limite A.
3
1
Slimslim n
n
n
n 
Le procédé que l’on vient d’employer pour déterminer A peut se reprendre pour toutes
fonctions continues et positives.
I] Intégrale d’une fonction positive :
f est une fonction continue et positive sur
b,a
avec
ba 
.
On appellera domaine associé à f sur
[a,b], le domaine plan D limité par la
courbe, l’axe des abscisses et les droites
d’équation
ax 
et
bx 
.
On peut aussi écrire que
xfy0
bxa
D
y
x
M
.
Le plan étant muni du repère orthogonal
j,i,O
l’unité d’aire est l’aire du rectangle bâti sur
ce repère.
Exemple :
D est le domaine associé à
2
xx:f 
sur
1,0
.
3
1
DA 
(en unité d'aire).
1) Définition :
Soit f une fonction continue et positive sur
b,a
avec
ba 
. On appelle intégrale de a à b de
la fonction f, l’aire du domaine associé à f sur
b,a
(en unité d'aire).
Ce nombre est noté
b
adx)x(f
.
Remarques :
 a et b sont les bornes de l’intégrale et
0dx)x(f
a
a
 x est une variable muette :
...du)u(fdt)t(fdx)x(f b
a
b
a
b
a 
Exemples :
1) Calculer
5
1
1dx3I

Soit
1
D
le domaine limité par
3x:f 
, l’axe
des abscisses, et les droites d’équation
1x 
et
5x 
.
Donc
1243153dx3I 5
1
1 
unité
d'aire.
2) Calculer
 3
21
2dx)1x2(I
f définie sur IR par
1x2)x(f 
.
Soit
2
D
le domaine limité par
1x2x:g 
, l’axe des
abscisses et les droites d’équation
2
1
x
et
3x 
.
f est continue et positive sur
3,
21
Donc
25,12
4
49
2
7
2
7
I
2
132
2
1
3
dx1x2I
2
3
21
2
3) Calculer
 5
0
3dx)2x(I
h définie sur IR par
2x)x(h 
Soit
3
D
le domaine limité par
2xx:h 
,
l’axe des abscisses et les droites d’équation
0x 
et
5x 
.
h est continue et positive sur
5,0
.
Donc
5,2225,242
2
49
2
277
I
222 2725
dx)2x(I
3
5
0
3
1
5
3
3
2
1
0

4) Calculer
dxx1I 1
12
4
i est définie sur
1,1
par
2
x1)x(i 
C la courbe qui représente i dans un repère
orthonormal.
2
x1yC
y
x
M
avec
1x1 
22 x1y 
avec
1x1 
et
0y 
222 1xy 
avec
1x1 
et
0y 
C est le demi disque de centre O et de rayon 1 situé dans le demi plan défini par
0y 
.
i est continue et positive sur
1,1
.
Donc
dxx1I 1
12
4
est l’aire du domaine associé à i sur
1,1
Donc
2
I4
2) Valeur moyenne :
f est continue et positive sur
b,a
avec
ba 
.
La valeur moyenne de f sur
b,a
est
 b
adx)x(f
ab 1
. est un réel positive qui vérifie
 b
adx)x(fab
.
f est continue sur
b,a
, donc
b
adx)x(f
est l’aire du domaine
associée à f sur
b,a
en unité
d'aire.
ab
est l’aire du rectangle
hachuré en rouge.
3) Extension aux fonctions de signe quelconque :
 f est continue et négative sur
b,a
avec
ba 
.

Le domaine associé ) f sur
b,a
est le
domaine plan D limité par la courbe, l’axe
des abscisses et les droites d’équation
ax 
et
bx 
.
Par ailleurs
0y)x(f
bxa
D
y
x
M
.
Par définition
)D(airedx)x(f
b
a
Exemple : Calculer
25
1dx1x
f est définie sur IR par
1x)x(f 
.
f est constante et négative sur
2
5
,1
Donc
25
1dx)x(f
est l’opposé de l’aire du
domaine associé à f sur
2
5
,1
(en unité d'aire).
 f est continue et de signe quelconque sur
b,a
avec
ba 
.
Dans ce cas
321
b
aEaireEaireEairedx)x(f 
.
Exemple :
Calculer
4
0dxx3
f définie sur IR par
x3)x(f 
f change de signe en 3.
2
5