Théorème des accroissements finis

!"
#"
$"
f
!"
#"
%"
&'!("
&'#("
&'!()&'#("
!)#"
•"
•"
!"
#"
$"
f
!"
#"
%"
&'!("
&'#("
&'!()&'#("
!)#"
•"
•
"
$%&'()*+",+-".//('0--+*+12-"3010-"
"
$%&'()*+"4",+-"566789::;<;=$:">9=9:"?"@'-+A%"B'C0-""B.D(.1D+"EFGHIEJEGK
" "
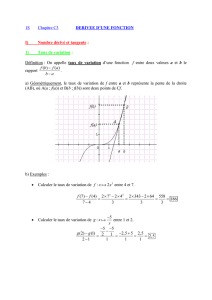
Entre&2&points&a&et&b,&selon&certaines&conditions,&il&existe&un&point&où&la&pente&de&la&tangente&
est&la&même&que&la&pente&de&la&droite&entre&a&et&b&
"
:0" " "f"*+,"-(""$./,0/1*"+12"3#4"!54""
" " " 6("78209#!:*"+12"5#4"!"3""
5L'(-"" " 0:"*%0+,*"1/"/.;!2*"$"7#/+"5#4"!"3"",*:"<1*"
() ()
'( ) fb fa fc ba
−
=
−
""
"
"
"
"
"
"
"
"
"
"
9LLC-2(.20'1"D(.A%0MC+! !
! ! ! ! !
=10+<1*"
() ()fb fa
ba
−
−
"2*>28+*/,*":#">*/,*"7*":#"72.0,*"*/,2*"#"*,"!"*,"<1*""
f&'(c)"*+,":#">*/,*"7*":#",#/?*/,*"@"f"*/"'$A&'$((4":*",B8.2C;*"7*+"#$$2.0++*;*/,+"&0/0+"
0/70<1*"<1D0:"*%0+,*"#1";.0/+"1/*"9#:*12"$"*/,2*"#"*,"!",*::*"<1*"L."A+12+",+"L."2.1D+12+"
N"f".C"A'012",O.P-/0--+"/"+-2"&D.L"N"L."A+12+",+"L.",('02+"+12(+"."+2"PQ""
"
R&*'1-2(.20'1"
E.0,"f&1/*"&./$,0./"+#,0+&#0+#/,":*+"BF>.,BC+*+G"
"
"
"
"
"
"
"
"
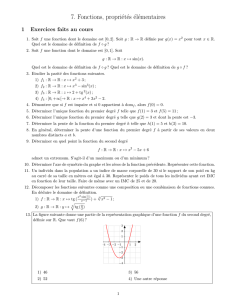
H<1#,0./"7*":#"+8$#/,*"d">#++#/,">#2"'#A&'#(("*,"'!A&'!(("I""
( )
f(b) f(a)
d(x) x a f (a)
ba
−
=−+
−
"
=.+./+"ϕ?SK"TU"3?SK"I",?SK"""'ϕ"*+,"1/*"&./$,0./"#1%0:0#02*"<10"*+,"78&0/0*"$.;;*":#"
70+,#/$*"#:?8!20<1*"*/,2*":*+"?2#>B0<1*+"7*"f"*,"7*"d("
"
"
"
"
"
&

f
%"
&'%("
d
7'%("
ϕ'%("
"
"
"
"
"
"
"
"
"
ϕ"+#,0+&#0,"#1%"BF>.,BC+*+"71",B8.2C;*"7*"JKLLM"$#2"I"
" " ϕ'#("N"ϕ'!("N"O"
" " ϕ"*+,"$./,0/1*"+12"3a;b5"
" " ϕ"*+,"78209#!:*"+12"5a;b3"
P./$"0:"*%0+,*"1/"/.;!2*"$"∈"5a;b3",*:"<1*"ϕD'$("N"O"
"
K2"""
(x) f '(x) d'(x)
′
ϕ=−
"*,"
(c) 0
′
ϕ=
4"#:.2+"
f(c) d'(c) 0 f(c) d'(c)
′′
−=⇒=
"
*,"$.;;*"
f(b) f(a)
d'(c) ba
−
=
−
"./"#"
f(b) f(a)
f(c) ba
−
′=
−
G" " "
" " " " " " " " " " "
" " " " " " " " " " "
!
""
"
"
"