1 Nombre dérivé 2 Tangente à une courbe en un point

Chapitre 0 4 : Nombre dérivé et tangente
Nombre dérivé
Tangente à une courbe en un point
Dérivées des fonctions usuelles
NOMBRE DERIVE ET TANGENTE
1 Nombre dérivé
Soit
f
une fonction définie sur un intervalle
I
et
a
un réel de
I
.
Soit
h
un réel non nul tel que
a+h∈I
1.1 Taux d'accroissement
➢Le taux d'accroissement de
f
entre
a
et
a+h
est le quotient :
f
(
a+h
)
−f
(
a
)
h
Exemple
Le taux d'accroissement de la fonction
f
définie par
f
(
x
)
=x2
entre
1
et
1+h
est :
f
(
1+h
)
−f
(
1
)
h=
(
1+h
)
2−12
h=1+2h+h2−1
h=2h+h2
h=2+h
1.2 Définition
➢On dit que la fonction
f
est dérivable en
a
lorsque le taux d'accroissement devient aussi
proche que l'on veut d'un nombre réel
L
lorsque
h
tend vers
0
.
➢Le nombre
L
est alors appelé le nombre dérivé de la fonction
f
en
a
et on le note :
L=f '
(
a
)
=lim
h→0
f
(
a+h
)
−f
(
a
)
h
Exemple
Le nombre dérivé de la fonction
f
définie par
f
(
x
)
=x2
en
1
est :
f '
(
1
)
=lim
h→0
f
(
1+h
)
−f
(
1
)
h=lim
h→0
2+h=2
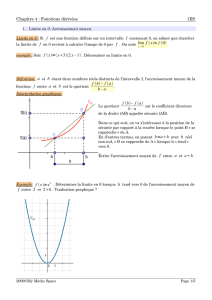
1.3 Interprétation graphique
Le taux de variation entre
a
et
a+h
peut être
vu comme le coefficient directeur de la droite
passant par les points
A
(
a;f
(
a
)
)
et
B
(
a+h;f
(
a+h
)
)
Lorsque
h
tend vers
0
, le point
B
se rapproche
du point
A
et les coefficients directeurs des
sécantes
(
AB
)
tendent vers
L
qui est le
coefficient directeur de la tangente
Δ
à la courbe
au point A.
2 Tangente à une courbe en un point
Soit
Cf
la courbe représentant une fonction
f
dérivable en a.
➢La tangente à
Cf
au point
A
(
a;f
(
a
)
)
a pour coefficient directeur
L=f '
(
a
)
➢La tangente à
Cf
au point
A
(
a;f
(
a
)
)
a pour équation :
y=f '
(
a
)(
x−a
)
+f
(
a
)
Exemple
Soit la fonction
f
définie par
f
(
x
)
=x2
et
Cf
sa courbe représentative dans un repère
(
O;⃗
i,⃗
j
)
orthonormal.
La tangente
Δ
à
Cf
au point d'abscisse
1
est :
Le coefficient directeur est
f '
(
1
)
=2
(voir précédemment) donc
Δ
a pour début d'équation :
y=2x+b
Δ
passe par le point d'abscisse
1
qui appartient à
Cf
, donc par le point
A
(
1 ; 12
)
donc
A
(
1 ;1
)
1=2×1+b⇔b=1−2⇔b=−1
. Donc
Δ
a pour équation :
y=2x−1
f(a)
a
f(a + h)
Oa + h
A
B
∆

3 Fonctions dérivées
3.1 Définition
➢Si une fonction
f
définie sur un intervalle
I
est dérivable en toute valeur
x
de
I
,
alors on dit que
f
est dérivable sur
I
.
➢La fonction qui, à tout
x
de I, associe le nombre dérivé de f en x s'appelle fonction
dérivée de
f
et se note
f '
3.2 Fonctions dérivées des fonctions usuelles
➢Les fonctions de références (sauf la fonction valeur absolue) sont dérivables sur tout
intervalle inclus dans leur ensemble de définition.
➢Les fonctions polynômes sont dérivables sur
ℝ
.
Sauf rares exceptions (la fonction racine carrée par exemple), toutes les fonctions que
vous aurez à étudier sont dérivables sur leur ensemble de définition.
f
(
x
)
f '
(
x
)
Df '
k
constante 0
ℝ
x
1
ℝ
ax+b
a
ℝ
x2
2x
ℝ
xn
n∈ℕ
n x n−1
ℝ
1
x
−1
x2
]
−∞; 0
[
∪
]
0 ;+ ∞
[
1
xn
n∈ℕ
−n
xn+1
]
−∞; 0
[
∪
]
0 ;+ ∞
[
√
x
1
2
√
x
]
0 ;+ ∞
[
3.3 Propriétés
➢Soit
u
et
v
deux fonctions dérivables sur un intervalle
I
Soit
k
un réel.
➢Le produit de la fonction
u
par un réel
k
est une fonction dérivable sur
I
.
(
k u
)
'=k u'
➢La somme de ces deux fonctions est dérivable sur
I
.
(
u+v
)
'=u' +v'
➢Le produit de ces deux fonctions est dérivable sur
I
(
u×v
)
'=u' ×v+u×v'
➢Le quotient de ces deux fonctions est dérivable sur
I
(
u
v
)
'=u'×v−u×v'
v2
Exemple
La fonction
u
définie sur
ℝ
par
u
(
x
)
=x2
est dérivable sur
ℝ
et
u'
(
x
)
=2x
La fonction
f
définie sur
ℝ
par
f
(
x
)
=8x2=
(
8u
) (
x
)
est dérivable sur
ℝ
et
f '
(
x
)
=8u'
(
x
)
=8×2x=16 x
v'
(
x
)
=5x4
et la fonction
g
définie sur
ℝ
par
g
(
x
)
=
(
u+v
)(
x
)
est dérivable sur
ℝ
et
g'
(
x
)
=u'
(
x
)
+v'
(
x
)
=2x+5x4
.
La fonction définie sur
ℝ−
{
0
}
par
h
(
x
)
=2x+1
x
est dérivables sur
ℝ−
{
0
}
et
h'
(
x
)
=2×x−
(
2x+1
)
×1
x2=2x−2x−1
x2=− 1
x2
1
/
2
100%