1 - DÉRIVATION DE FONCTION I. NOMBRE DÉRIVÉ ET

DMartin-LAH
-
1
-
DÉRIVATION DE FONCTION
I. NOMBRE DÉRIVÉ ET TANGENTE
Idée générale : Soit f une fonction définie sur un intervalle I.
Dans l’optique d’étudier les variations de cette fonction nous allons chercher à approximer localement la courbe de f par
une droite, c'est-à-dire à approximer la fonction f par une fonction affine et ce en chaque point de la courbe.
Définition
:
Soit a un nombre réel appartenant à I. Soit une fonction f définie en a et au voisinage de a.
La fonction f est dérivable en a si et seulement si il existe un nombre réel L tel que :
h
)a(f)ha(f
h
−
+
→0
lim
= L
Définitions : • Le nombre hafhaf )()( −+ est appelé le taux d’accroissement de f entre a et a + h.
• Si
h
)a(f)ha(f
h
−
+
→0
lim
n’est pas un nombre réel alors on dit que f n’est pas dérivable en a.
Aspect géométrique de la dérivée : tangente à la courbe en un point (exemple)
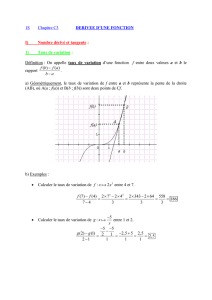
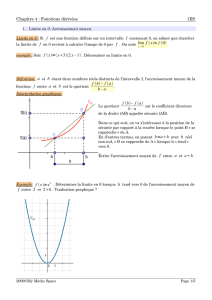
On a tracé ci-contre la courbe représentative  de la fonction
définie sur  par : f(x) = x
2
– x
La droite T est la tangente à  en 1.
M
1
et M
1+h
sont les point de  d’abscisses 1 et 1 + h.
On considère la corde (M
1
M
1+h
), en pointillés sur le graphique.
1. Déterminer graphiquement le coefficient directeur de T :
2. Déterminer en fonction de h :
• Les coordonnées de M
1+h
:
• Le coefficient directeur de (M
1
M
1+h
) :
3. Calculez la limite de ce coefficient directeur lorsque h tend vers 0 : Que représente-t-il ?
4. Quel est le signe de f '(1) ? Que peut on en déduire, localement en 1, pour la fonction f ?
Théorème : Soit a un nombre réel. Soit une fonction f dérivable en a de représentation graphique .
Le coefficient directeur de la tangente à  au point M
a
d’abscisse a est égal au nombre dérivé de f en a.
Théorème : L’équation de la tangente à  au point M
a
d’abscisse a est : y =
)(af
′
(x – a) + f(a)
Exemple : Donner l’équation de la tangente T dans l’exemple ci-dessus.
Définition : Dans les conditions du théorème précédent, on appelle L le nombre dérivé de f en a. On note :
)a(f
′
= L
0 1
1
x
y
Lorsque h tend vers 0 :
• le point M
1+h
« se déplace » vers le point M
1
.
• La droite (M
1
M
1+h
) se déplace de la même manière
pour atteindre comme position limite la tangente T.
T
1 + h
M
1
M
1+h

DMartin-LAH
-
2
-
II. FONCTIONS DÉRIVÉES
Exemple :
Soit la fonction f définie sur  par : f(x) = x
2
. Soit x
∈
 quelconque et soit h non nul, alors :
f(x + h) – f(x)
h =
Lorsque h tend vers 0 : 0 lim
→h =
Quelle que soit la valeur de x dans IR ce calcul est valable et la limite est finie.
Nous pouvons donc affirmer que la fonction carré : f(x) = x
2
est dérivable sur et que sa fonction dérivée est la
fonction :
f
′
: 
→
x
a
)(xf
′
=
Exercice :
Déterminer l’ensemble de dérivation et les fonctions dérivées des fonctions suivantes :
f définie sur par : f(x) = k f définie sur par : f(x) = x f définie sur R
*
par : f(x) =
Avec k ∈ R .
Théorème : Dérivées des fonctions usuelles
Le tableau ci-dessous donne les dérivées de certaines fonctions usuelles. Les résultats non démontrés précédemment
seront admis ou traités en exercice.
Ensemble de
définition
*
[0 ; + ∞ [
Fonction f(x) k x x
2
x
3
x
n
n
∈
*
1
x x mx+p
m,p
∈
R
ax
2
+bx+c
a,b,c
∈
R
Fonction
Dérivée
)(xf
′
3 x
2
n x
n – 1
m 2 ax + b
Ensemble de
dérivation
Définition : Soit une fonction f dont l’ensemble de définition est un intervalle ou une réunion d’intervalles.
Soit
1
l’ensemble de tous les réels x de tels que f soit dérivable en x . (
1
⊂ )
On dit alors que f est dérivable sur
1
.
On appelle fonction dérivée de f la fonction
f
′
qui à tout réel x de
1
associe le nombre dérivé de f en x .
On note :
f
′
: 
1
→
x
a
)(xf
′

DMartin-LAH
-
3
-
Propriétés : Opérations sur les fonctions dérivables
Soit u et v deux fonctions dérivables sur un intervalle I, soit k un nombre réel et soit n ∈ IN.
Fonction Dérivée Ensemble de
dérivation Exemple
u + v u’ + v’ I [ x
2
– 1
x ]’ = [ x
2
] ’ – [ 1
x ]’ = 2x + 1 x
2
k u avec k
∈
k u’ I [ 5x
2
]’ = 5 × [ x
2
]’ = 5 × 2x = 10x
u v u’ v + u v’ I [x x]’ = [ x ]’ x + x [ x ]’ = x + x
2 x = 3
2 x
v
1
2
v
v
′
−
I \ { v(x) = 0} [
1
x
2
] ’= –
2 x
(x
2
)
2
= – 2
x
x
4
= – 2
x
3
v
u
2
v
uvvu ×
′
−×
′
I \ { v(x) = 0} [
x + 1
2 x – 1]
’ =
1 × (2 x – 1) – 2 × ( x + 1)
(2 x – 1)
2
= – 3
(2 x – 1)
2
u
2
2u’u I [(3 x + 1)
2
] ’ = 2 × 3 × (3 x + 1) = 18 x + 6
Exercices :
1. Pour chaque fonction donnée en exemple dans le tableau ci-dessus, déterminer l’ensemble sur lequel elle est dérivable
2. Pour chacune des fonctions suivantes, déterminer son ensemble de dérivabilité puis calculer sa fonction dérivée.
a(x) = 3
2
x
4
– 5
6
x
3
– 4 x + 3 b(x) = 5 x – 3
x
c(x) = ( x
2
– 3)(3 – 2 x
2
) (sans développer)
d(t) = 7
t – 3
1 – 9 t
e(x) = –4
7 x
2
+ 1
III. DÉRIVÉE ET SENS DE VARIATION D’UNE FONCTION
1. Signe de la dérivée et sens de variation
Théorème : Soit une fonction f définie et dérivable sur un intervalle I.
Si, pour tout x
∈
I, f '(x) = 0, alors f est constante sur I.
Si, pour tout x
∈
I, f '(x)  0, alors f est décroissante sur I.
Si, pour tout x
∈
I, f '(x) 0 , alors f est croissante sur I.
Exercice : Etudier les variations d’une fonction
Soit la fonction f définie sur R par f(x) = x
3
– 3 x
2
–24 x + 12
1. Etudier les variations de f et dresser son tableau de variation.
2. Dans repère orthogonal aux unités judicieusement choisies, représenter graphiquement la fonction f .
2. Extremum d'une fonction
Théorème : Soit une fonction f définie et dérivable sur un intervalle ouvert I.
Si la dérivée f ' de f s'annule et change de signe en un réel c de I alors f admet un extremum en x = c .
Exercice :
La fonction f définie sur R par f(x) = – x
3
+ 3 x
2
+ 9 x – 4 admet-elle des extrema sur R ?