6 derivation

1
6. DERIVATION
A. Nombre dérivé :
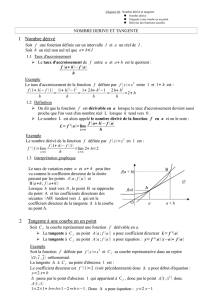
1. Taux d’accroissement d’une fonction entre a et a + h
Définition :
On appelle de f entre a et a + h le quotient :
Exemple : Déterminer le taux
d’accroissement entre 3 et 3+h de la fonction
carrée définie sur ℝ .
2. Nombre dérivé de la fonction f en a.
Définition : Si le quotient : tend vers un nombre réel lorsque h
se rapproche de 0 ; on dit que f est

2
B. Tangente :
Propriété : Si f est dérivable en a et de nombre dérivé f ’ (a) en a, alors f ’ (a) est :
En particulier, est :
C. Fonction dérivée :
Soit f une fonction dérivable en tout point d’un intervalle I. On dit alors que f est dérivable
sur I.
On appelle
la fonction qui à tout nombre réel x de I associe le nombre dérivé de f en x.