Chapitre 7 - Canalblog

(suite du chapitre 6)
Inéquations du type ax+b>cx+d
Et
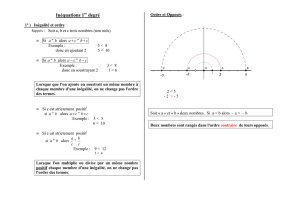
Représentation des solutions sur une droite graduée
III) Ordre et opérations :
1) Addition ou soustraction :
Propriété : a, b et c étant des nombres, a+c et b+c
sont rangés dans le même ordre que a et b.
(par exemple : si a<b alors a+c<b+c)
Autrement dit : on peut ajouter ou retrancher le
même nombre aux deux membres d’une
inégalité sans en changer le sens.
Exemples : résoudre les inéquations suivantes
2
53
x
x
1
34
y
y
2) Multiplication ou division :
Propriété : a, b et c étant des nombres,
 si c>0 alors a c et b c sont rangés dans
le même ordre que a et b
 si c<0 alors a c et b c sont rangés dans
l’ordre inverse de a et b
Autrement dit : lorsqu’on multiplie ou on divise les
deux membres d’une inégalité par le même
nombre non nul :
 on garde le sens de l’inégalité si ce nombre
est strictement positif
 on change le sens de l’inégalité si ce
nombre est strictement négatif
Exemples : résoudre les inéquations suivantes