Inéquations

Chapitre. Inéquations du premier degré.
On peut ajouter ou retrancher un même nombre à chaque membre d’une inégalité sans changer le signe de
l’inégalité.
Si a < b, alors a + c < b + c.
a  c > b  c
Quand on multiplie ou qu'on divise chaque membre d'une inégalité par un nombre strictement positif, on ne
change pas le signe de l'inégalité.
Quand on multiplie ou qu'on divise chaque membre d'une inégalité par un nombre strictement négatif, on
change le signe de l'inégalité.
Si b < c, alors ab < ac si a > 0.
ab > ac si a < 0.
Résoudre une inéquation d'inconnue x, c'est chercher toutes les valeurs de x vérifiant cette inégalité.
remarque 1: Il y a souvent plusieurs solutions.
Résoudre: 5x ≤ 2
cela revient à chercher les nombres x tels que 5 x
5 ≤ 2
5 (5 > 0) ,
soit x ≤ 2
5 ,
Les solutions de cette inéquations sont les nombres x tels que: x ≤ 2
5 .
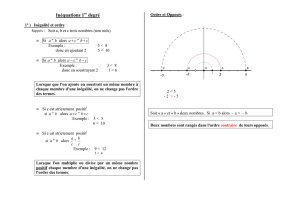
représentation graphique des solutions:
résoudre - 3 x < 9
cela revient à résoudre - 3 x
- 3 > 9
-3 (− 3 < 0, on doit changer le signe)
2
5
soit x > - 3
Les solutions de cette inéquation sont les nombres x tels que: x > 3.
3
Attention, il faut préciser si on représente en couleur l’ensemble des solutions ou les nombres qui ne sont
pas solutions.