1ères S - KerMaths

1ères S
Mathématiques : devoir n°4(2h)
12/12/01
NOM :……………………. Prénom :………………………..
Exercice 1 (9 points)
Pour chaque question, il y a plusieurs propositions.
Indiquer pour chacune d’elles uniquement si elle est vraie ou fausse (il peut y avoir aucune ou
plusieurs réponses vraie(s) ).
Barème : bonne réponse 1 point ; réponse fausse : - 0,75 point ; pas de réponse : 0 point.
Question
Proposition
Réponse
A. f est la fonction définie par
2
13
)(  xx xf
C est sa courbe représentative dans un repère
(O ;
j,i 
).
1. La fonction f est croissante sur
]– ;–2[]–2;+[.
2. La tangente à la courbe C au point
d'abscisse –1 a pour équation
27  xy
.
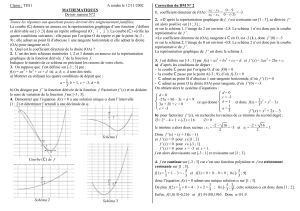
B. f est une fonction définie sur . La courbe
ci-dessous est la représentation graphique
de la fonction f', dérivée de la fonction f.
C est la courbe représentative de f dans un
repère (O ;
j,i 
).
1. La fonction f est décroissante sur
l'intervalle ]– ;1[.
2. La fonction f est décroissante sur
l'intervalle [–1;3].
3. L'équation de la tangente à C au
point d'abscisse 0 est
32  xy
4. La courbe C admet une tangente
horizontale au point d'abscisse 3.
C. La courbe C est la représentation graphique
d'une fonction f dérivable sur .
Les droites tracées sont tangentes à la courbe C.
1. f(1) = 0 et f '(1) = – 3
2. L'équation f '(x) = 0 admet deux
solutions dans .
3. La dérivée de la fonction f est :
f '(x) = –3x² + 6x
C
o2
-2
2
I
J
o
-2 2 4
-4
-2
2

Exercice 2 (6 points)
Pour chacune des fonctions f suivantes, calculer la dérivée f'(x):
a)
²
5
4)( x xxf 
b)
4
²)1(3)( xxf 
c)
13 4²
)(  xxx xf
Exercice 3 (15 points)
On considère la fonction f définie sur  par :
132
3
1
)( 23  xxxxf
On désigne par () la courbe représentative de f dans un repère
);;( jiO 
.
1. Calculer la dérivée
)(' xf
, étudier son signe, puis dresser la tableau de variation de la fonction f.
2. Déterminer l'équation de la droite (T) tangente à la courbe () au point d'abscisse 2.
Etudier la position relative de () et de (T).
3. Montrer que le point I( 2 ;
3
1
) est centre de symétrie de la courbe ().
4. Construire la courbe () et la droite (T).
5. Montrer que l'équation
0)( xf
admet trois solutions.
Donner, en justifiant la réponse, un encadrement de la plus petite des solutions à
4
10
près.
Exercice 4 (10 points)
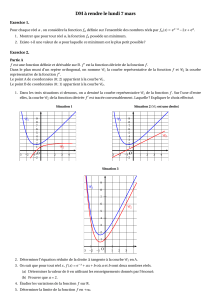
T
La courbe ci-contre représente une fonction f définie et
dérivable sur [0 ; 4] dans un repère orthonormal..
La droite (T) est tangente au point A d'abscisse 0.
La courbe admet une tangente parallèle à l'axe des
abscisses au oint d'abscisse 1.
1. a) Donner f(0) , f(1) , f '(0) et f '(1).
b) donner le tableau de variation de la fonction f.
2. On considère la fonction g inverse de la fonction f,
c'est à dire
g
f1
. On note g' la dérivée de la
fonction g.
a) Déterminer g(0) , g(1) et g(3).
b) Déterminer les valeurs g '(0) et g '(1).
c) Déterminer le sens de variation de g. Justifier.
d) Construire sur le graphique la courbe
représentative de g.
o2 4
-1
1
2
3
I
J
A