I Valeur exacte et valeurs approchées d`un quotient :

ATTENTION : On ne peut jamais diviser un nombre par ………………………………..
I Rappel :
Définition : Le nombre qui, multiplié par
b
(…………..), donne
a
est …………………..
cad : …………………………………………………………..
Il existe alors 2 cas :
 La division de
a
par
b
se termine. Le quotient
b
a
est alors un nombre ………………..................
On peut donc donner une écriture……………………………………………………………. du quotient
b
a
Exemple :
4
17
…………………….
Cas particulier :Lorsque le quotient
b
a
est un nombre entier, on dit que
a
est ……..……..……………par
b
ou que :
a
est un ………………..…..……….de
b
ou que :
b
est un ………………..…..……….de
a
ou que :
b
………….……………..…..……….
a
 La division de
a
par
b
ne se termine pas. Le quotient
b
a
n’est pas un nombre ……………………
La seule façon décrire la valeur exacte de ce quotient est alors ………………………………………
On peut donner des écritures décimales …………………………..…………………… du quotient
b
a
.
Exemple : Considérons le quotient
7
11
.
La calculatrice affiche : ……………………………………………………………………………………………
La division de 11 par 7 ………………………………………………
Nous ne pouvons donc donner des valeurs ………………………………ou ………………..………..……….
décimales de
7
11
.
QUOTIENTS

Troncature
Encadrement
Schéma
Arrondi
(valeur approchée la plus proche du nombre)
A l’unité
……………
………………..…
On regarde le chiffre des……………..........................
Donc l’arrondi à l’unité est : ………………………..…..
Au dixième
……………
………………..…
On regarde le chiffre des……………..........................
Donc l’arrondi au dixième est : …………………………
Au centième
……………
……………...……
On regarde le chiffre des ………….………….……….
Donc l’arrondi au centième est : …..……….…………
Au millième
…………
……………….......
.
On regarde le chiffre des ………….…………………..
Donc l’arrondi au millième est : …..……..………….
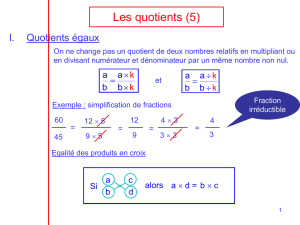
II Comment savoir si des quotients sont égaux ?
1) Propriété des quotients égaux :
Un quotient ne change pas si on ………………………………. ou …………………………………. le
numérateur et le dénominateur par un même nombre ………………………………….
En langage mathématique :
On considère 3 nombres relatifs
a
,
b
et
k
avec
0k
et …………………….
..........................................
b
a
Cas particuliers :
............................
b
a
et
.......................................... 
b
a
A quoi ça sert ? A simplifier des quotients…
Pour cela, il faut absolument connaître les critères de divisibilité suivants :

Un nombre est divisible par 2 lorsqu’il se finit par ………….………………………………………………
On dit alors que c’est un nombre …………...
Ex :
Un nombre est divisible par 3 (respectivement par 9) lorsque ………….…………………………………
……………………………………………………………………………………………………………………..
Ex : ………………….……… est divisible par 3 car …………………………………………………………
…………………………. n’est pas divisible par 9 car ………………………………………………….
Un nombre est divisible par 5 lorsqu’il se finit par ……………………………………………………….
Ex :
Un nombre est divisible par 10 lorsqu’il se finit par ……………………………………………………
Ex :
Exemples : Simplifier « au maximum » les fractions suivantes :
36
28
A
120
105
B
…………………………..……… 1ère étape : on s’occupe du signe du quotient …………………………………
………………………………… 2ème étape : on cherche un diviseur commun ………………………………
au numérateur et au dénominateur
………………………………… 3ème étape : on continue jusqu’à ne plus pouvoir …………………………………
diviser le numérateur et le dénominateur
par le même nombre entier
………………………………… ………………………………….
Vocabulaire : On dit que ……………………..………sont des fractions …………………………………
Cela veut dire que l’on ne pleut plus les ………………………………………..
2) Egalité des produits en croix :
Propriété : On considère 4 nombres relatifs
a
,
b
,
c
et
d
avec
0b
et
0d
.
(1) Si
d
c
b
a
Alors ………………………………
Réciproque : (2) Si . …………… Alors ……………………………..
Démontrons (1) :
On suppose que : ………………………………..
………………………………………………………………………….
…………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………

Démontrons (2) :
On suppose que : ……………………………………
On va diviser les 2 membres de cette égalité par …………………………….
……………………………………………………………………………………….
……………………………………………………………………………………….
Applications :
1) Trouver le nombre
x
tel que :
2
75
x
.
…………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
2) Les quotients
3
2
et
3,1
4,5
sont-ils égaux ? Justifier.
………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
III Comment additionner et soustraire des quotients ?
Dans tous les exemples suivants, on donnera les résultats sous forme de quotients irréductibles
1) 1er cas : Si les dénominateurs sont identiques
Pour additionner (ou soustraire) 2 quotients ayant le même dénominateur, il suffit
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
En langage mathématique : On considère 3 nombres relatifs
cba ,,
tels que :
0c
................................................... c
b
c
a
................................................... c
b
c
a
Applications :
58
99
......................................
......................................
......................................
......................................
A
25
77
......................................
......................................
......................................
......................................
B  

2) 2ème cas : Si les dénominateurs sont différents
Pour additionner (ou soustraire) 2 quotients n’ayant pas le même dénominateur, il faut d’abord
…………………………………………………………………………………………………………………….
Pour cela, il faut chercher un ………………………………………………………………………………….
……………………………………………………………………………………………………………………..
Applications :
34
14 7
A
72
53
B
57
64
C  
……………………………………………………………………………………..……………………………….
……………………………………………….…………………………………………………..………………….
……………………………………………….…………………………………………………..…………………..
……………………………………………….…………………………………………………..…………………..
……………………………………………………………………………………………………….……………….
………………………………………………………………………………………………………………………..
IV Comment multiplier des quotients ?
Remarque : Pour multiplier des quotients, il n’est pas nécessaire d’avoir ………………………………………………
Il faut toujours penser à simplifier avant de multiplier !!
Exemples :
3
5
67
C
15 14
7 25
D
Pour multiplier deux quotients, on ……………………………………………………………………….…
……………………………………………………………………………………………………………………
En langage mathématique :
On considère 4 nombres relatifs
cba ,,
et
d
avec
0b
et
0d
.
............................................... d
c
b
a