Quotients en écriture fractionnaire Egalités de quotients

Quotients en écriture fractionnaire
Définition (rappel) : Soient a et b deux nombres relatifs avec   .
Le quotient de a par b est le nombre qui multiplié par b donne a (*).
Le quotient de a par b se note  ou 
La phrase (*) se traduit alors mathématiquement par : 
Complète les égalités suivantes :
Egalités de quotients
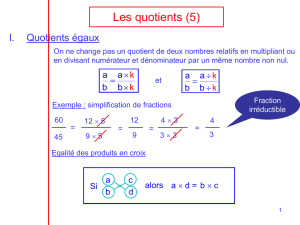
Propriété : Un quotient ne change pas quand on multiplie ou que l’on divise son numérateur est son
dénominateur par un même nombre différent de 0.
Soient a, b et k trois nombres avec   .
On a : 
 et 
Complète les égalités suivantes :
Simplification de quotients
Définition : Simplifier une fraction, c’est écrire une fraction qui lui est égale avec un numérateur et un
dénominateur plus petits. Pour cela, on utilise les critères de divisibilité.
Simplifier les fractions suivantes :

Comparaison, addition et soustraction de quotients
Propriété : Pour comparer deux nombres relatifs en écriture fractionnaire avec des dénominateurs
différents, on les écrit avec le même dénominateur (on dit qu’on les réduit au même dénominateur) puis on
compare leurs numérateurs.
Comparer :
 et   et   et   et   et   et 
Comparer après avoir pensé à simplifier leur écriture :
 et   et 
 et 
Propriété : Pour additionner ou soustraire deux nombres en écriture fractionnaire qui n’ont pas le même
dénominateur :
 On les écrit avec le même dénominateur
 On additionne ou on soustrait les numérateurs
Calculer et simplifier le résultat si possible :

Multiplication de quotients
Propriété : Pour multiplier deux nombres en écriture fractionnaire :
 On multiplie les numérateurs entre eux
 On multiplie les dénominateurs entre eux
Soient a, b c et d quatre nombres avec    et   .
On a : 
Calculer :
Inverses
Définition : Deux nombres relatifs non nuls sont inverses quand leur produit est égal à un.
Soient a et b deux nombres relatifs non nuls.
L’inverse de a est 
 car 
L’inverse de 
 est   car 
Déterminer les inverses des nombres suivants :
Division de quotients
Propriété : Diviser par un nombre relatif non nul revient à multiplier par son inverse.
Soient a, b, c et d quatre nombres relatifs avec   , c  et d .
On a :
 ce qui s’écrit aussi 
 ce qui s’écrit aussi 
Calculer :

Priorités opératoires
Calculer :
Puissances
Définitions et règles de calcul : Soient n et m deux nombres entiers relatifs.
Soient a et b deux nombres.
On a :
 (avec   ) 
 (avec  ) 
Ecriture scientifique
Définition : Tout nombre décimal non nul peut s’écrire
sous la forme   avec a un nombre
décimal non ne comportant qu’un seul
chiffre non nul avant la virgule et n un
nombre entier relatif.
Cette notation est appelée notation
scientifique d’un nombre décimal ou
écriture scientifique d’un nombre décimal
PGCD
Il existe deux méthodes pour calculer le PGCD :
 l'algorithme des soustractions
 l'algorithme d'Euclide