Loi normale

Loi normale
Rappels sur la loi binomiale :
1
11Situation
On répète nfois, de façon indépendante, la même expérience, à deux issues possibles :
•Succès, de probabilité p,
•Échec, de probabilité 1−p.
Exemple. On peut représenter cette situation par un arbre. Si n= 3 et p= 0,3, on a cet arbre :
•
Succès
Succès Succès
Échec
Échec
Succès
Échec
Échec
Succès Succès
Échec
Échec
Succès
Échec
0,3
0,3
0,3
0,7
0,70,3
0,7
0,70,3
0,3
0,7
0,70,3
0,7
12Loi binomiale
Dans la situation précédemment décrite, soit Xla variable aléatoire associée au nombre kde succès parmi
les nexpériences. Xprend toutes les valeurs entières entre 0et n.
Xest la variable aléatoire associée au nombre kde succès parmi les nexpériences
On dit que Xsuit la loi binomiale de paramètres net p. On note X → B(n;p).
Définition 1
Remarques.
•Les probabilités se calculent avec la calculatrice ou le tableur.
•P(X=k)est la probabilité d’obtenir exactement ksuccès parmi les nexpériences.
•P(X6k)est la probabilité d’obtenir au plus ksuccès parmi les nexpériences.
•P(X > k) = 1 −P(X6k).
Si Xsuit la loi binomiale de paramètres net p, alors son espérance est E(X) = np .
Théorème 1
Exemple. On lance 15 fois de suite une pièce de monnaie truquée : la probabilité d’obtenir « Pile » sur un
lancé est 0,3.
On s’intéresse à X, variable aléatoire égale au nombre de « Piles » obtenus.
On a donc X → B(15 ; 0,3) .
On construit un diagramme représentant cette loi : en abscisse, ce sont les valeurs kde la variable aléatoire
X(avec 06k615 ), et en ordonnée, les probabilités P(X=k).
http://lycee.lagrave.free.fr/cahiers 1

TSTMG. Loi normale
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
0,2
0,22
k
p(X=k)avec X → B(15 ; 0,3) kp(X=k)
0 0.00474756
1 0.03052003
2 0.09156010
3 0.17004020
4 0.21862313
5 0.20613039
6 0.14723600
7 0.08113004
8 0.03477002
9 0.01159001
10 0.00298029
11 0.00058058
12 0.00008294
13 0.00000820
14 0.00000050
15 0.00000001
On a donc E(X) = 15 ×0,3=4,5.
Loi normale :
2
21Approximation de la loi binomiale par une loi normale
Illustration : Soit Xune variable aléatoire suivant une loi binomiale de paramètres n= 50 et p= 0,3.
On construit un diagramme représentant cette loi : en abscisse, ce sont les valeurs kde la variable aléatoire
X(avec 06k650 ), et en ordonnée, les probabilités P(X=k).
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
0
0,02
0,04
0,06
0,08
0,1
0,12
k
p(X=k)
On remarque que le diagramme ressemble à une courbe « en cloche » . Cette courbe est celle d’une
fonction, appelée densité de probabilité, qui définit une nouvelle loi de probabilité, appelée loi normale.
22Courbe de la loi normale
La loi normale tire son nom du fait qu’elle est bien adaptée pour modéliser des phénomènes naturels
issus de plusieurs évènements aléatoires. On l’appelle aussi loi de Gauss-Laplace, du nom de 2 grands ma-
thématiciens l’ayant étudiée. Par exemple, la répartition des tailles d’individus dans une population peut
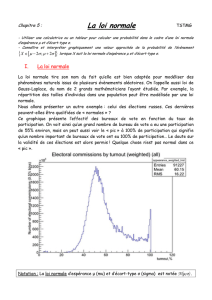
être modélisée par une loi normale. Nous allons présenter un autre exemple : celui des élections russes. Ces
dernières peuvent-elles être qualifiées de « normales » ? Ce graphique présente l’effectif des bureaux de vote
en fonction du taux de participation. On voit ainsi qu’un grand nombre de bureau de vote a eu une partici-
pation de 55% environ, mais on peut aussi voir le « pic » à 100% de participation qui signifie qu’un nombre
important de bureaux de vote ont eu 100% de participation . . . Le doute sur la validité de ces élections est
alors permis ! Quelque chose n’est pas normal dans ce « pic ».
2http://lycee.lagrave.free.fr/cahiers

TSTMG. Loi normale
Deux paramètres caractérisent une loi normale :
•Son espérance µ, égale à celle de la loi binomiale qu’elle approche, c’est-à-dire n×p.
•Son écart-type σ.
On dira alors qu’une variable aléatoire Xsuit une loi normale de paramètres µet σ.X → N (µ;σ2)
La probabilité P(a6X6b)est égale à l’aire du domaine compris entre la courbe de la loi normale,
l’axe des abscisses et les droites d’équation x=aet x=b.
Propriété 1
Exemple. La taille Xdes hommes en France est modélisée par la loi N(172 ; 142)
0,005
0,010
0,015
0,020
0,025
0,030
0 20 40 60 80 100 120 140 160 180 200 220 240 260
Méthode : On choisit au hasard un homme dans la population française.
a. Quelle est la probabilité qu’il mesure entre 1,60 m et 1,80 m ? On souhaite calculer P(160 < X < 180).
Casio : Graph 35+et modèles supérieurs TI82 Stats et modèles supérieurs
Menu STAT, puis DIST, et enfin NORM
•Calcul de P(a6X6b)→Ncd
avec pour valeurs : Lower : 160
Upper : 180
σ: 14
µ: 172
puis Calc (F1) . . .
2nd→DISTR (ou distrib)
•Calcul de P(a6X6b)→normalcdf (ou
normalFrep)
puis : normalcdf(160,180,172,14)
http://lycee.lagrave.free.fr/cahiers 3

TSTMG. Loi normale
À la calculatrice, on obtient : P(160 < X < 180) 'à10−4près soit 52,05%
Le domaine sous la courbe d’une loi normale a pour aire 1.
Hachurer sur la figure précédente, le domaine correspondant à P(160 < X < 180).
b. Quelle est la probabilité qu’il mesure plus de 2m ? On souhaite calculer P(200 < X).
À la calculatrice, on obtient : P(200 < X)'à10−4près soit 2,28%
on procède de même, en entrant la borne supérieure : 1E+99
Remarques. Pour P(X6b): on peut procéder de même, en entrant la borne inférieure : −1E+99.
•Pour n’importe quel k,P(X=k)=0 et par symétrie, on a P(X>µ) = P(X6µ)=0,5.
•P(X>a)=1−P(X < a)et P(a6X6b) = P(X6b)−P(X < a)
- L’espérance µ, est l’abscisse de l’axe de symétrie de la courbe Gaussienne (« en cloche »).
N(0 ; 12)N(−2 ; 12)N(2 ; 12)
3lois normales de même écart-type
- L’écart-type σ, mesure la dispersion des valeurs autour de l’espérance. Plus l’écart-type est grand et
plus les valeurs sont dispersées autour de l’espérance.
N(2 ; 12)N(2 ; 0,52)N(2 ; 22)
3lois normales de même espérance
23Résolution de problème sans calculatrice
Si Xest une variable aléatoire suivant une loi normale d’espérance µet d’écart-type σalors :
P(µ−2σ6X6µ+ 2σ)'0,954 soit 95,4%
Propriété 2
µ
µ−σµ+σ
µ−2σµ+ 2σ
'95%
Exemple. En France, la taille des femmes suit une loi normale d’espérance 163 cm et d’écart-type 6cm.
On choisit une femme au hasard.
a. Quelle est la probabilité que cette femme mesure entre 151 et 175 cm ?
4http://lycee.lagrave.free.fr/cahiers