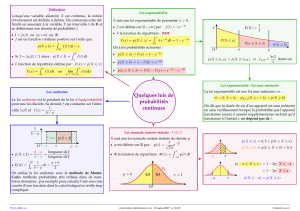
loi normale

5 La Loi de Laplace Gauss
ou loi Normale

1)Définition:
•a)On appelle loi normale
d’espérance mathématique met
d’écart type , notée m,),
la loi de probabilité d’une
variable aléatoire continue
telle que X()=et dont la
densité de probabilité f est

2
2
2)(
2
1
)(
mx
exf 

b)Cas particulier de N(0,1)
d’espérance mathématique 0 et
d’écart type 1:
•La loi normale centrée réduite N(0,1) a pour
densité f telle que
2
2
2
1
)( x exf 

2)Relation entre N(m,) et
N(0,1) :
•Si la v.a. continue X suit une loi normale
N(m,) alors la v.a. suit
•la loi normale centrée réduite N(0,1)
mX
T