les inequations

LES INEQUATIONS DU PREMIER DEGRE A UNE
INCONNUE
I DEFINITION
Une inéquation comporte une relation d’ordre :
soit « plus grand que » ou « supérieur à »
soit « plus petit que » ou « inférieur à »
Cette relation d’ordre peut être une relation d’ordre strict :
« strictement supérieur à » notée >
ou d’ordre large :
« supérieur ou égal à » notée ≥
Il existe de même la relation « strictement inférieur à » notée <
et « inférieur ou égal à » notée ≤
Pour résoudre une inéquation, il faut respecter les règles applicables aux inégalités.
II LES INEGALITES
Il faut bien comprendre que de deux nombres NEGATIFS,
le PLUS PETIT est celui qui a la PLUS GRANDE VALEUR ABSOLUE :
5 > 2 mais -5 < -2
Ceci entraîne un changement de sens de l’inégalité quand on passe de l’écriture en
nombres positifs à l’écriture en nombres négatifs.
C’est le cas de la multiplication des deux membres d’une inégalité par -1 et plus généralement
par un nombre négatif :
5 > 2
x (-4) x(-4)
ATTENTION !
5 ( -4) < 2 (-4) ON CHANGE LE SENS DE L’INEGALITE
- 20 < -8
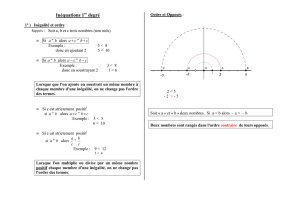
–5 –2 –1 0 1 2 5

Ainsi on retiendra :
Multiplier (ou diviser) les deux membres d’une inégalite par un même nombre NEGATIF
CHANGE le sens de cette inégalite.
Les autres règles applicables aux égalités, le sont aussi pour les inégalités :
1) L’addition ou la soustraction d’un même nombre aux deux membres d’une inégalité
ne change pas l’ordre.
2) La multiplication (ou la division) des deux membres d’une inégalité par un même
nombre POSITIF ne change pas l’ordre.
Par contre, l’addition membre à membre de deux inégalités est beaucoup plus complexe et
n’est pas au programme.
III RESOUDRE UNE INEQUATION
Ex : 2 a + 5 < 7 on transpose 5 dans l’autre membre
2 a < 7 – 5
2 a < 2 on divise par 2 sans changer l’ordre
a < 2/2
a < 1
Il y a UNE INFINITE DE SOLUTIONS : ce sont tous les nombres plus petits que 1.
Il est classique de représenter ces solutions sur le schéma de l’axe de tous les nombres réels :
On barre ce qui ne convient pas.
CONVIENT NE CONVIENT PAS
1 ne convient pas car 2a + 5 est strictement inférieur à 7 : on place un crochet sur 1 que
l’on tourne du côté des nombres qui ne conviennent pas.
On écrit : a Є ] - ; 1 [
Le crochet ouvert signifie que 1 ne convient pas
signifie
« appartient à » l’infini le point virgule signifie « jusqu’à »
les crochets signifient un ensemble de nombres
(il est toujours ouvert sur l’infini)
–5 –2 –1 0 1 2 5