Variables aléatoires, Estimation ponctuelle, Principes généraux sur

Variables aléatoires, Estimation ponctuelle,
Principes généraux sur les tests
Mémo 2015-2016
1 Rappels sur les variables aléatoires
Définition 1.1 (Loi de Bernoulli B(π))
C’est une une variable aléatoire discrète Xreprésentant une épreuve à deux issues qu’on appellera souvent
échec et succès en prenant uniquement les valeurs 0et 1avec les probabilités suivantes :
π=P(X=1) = P(succès)1−π=P(X=0) = P(échec)
C’est une variable d’espérance E(X) = π, et de variance V(x) = π(1−π).
01
0
0.2
0.4
0.6
0.8
1
Issue
Probabilités πet 1−π
Loi de Bernoulli B(0.6)
Définition 1.2 (Loi binomiale B(n,π))
C’est une variable aléatoire discrète Xreprésentant le nombre de succès lors la réalisation de népreuves de
Bernoulli indépendantes. Elle prend les valeurs 0, 1, 2, . . . navec les probabilités suivantes :
πk=P(X=k) = P(ksuccès parmi n) = Ck
nπk(1−π)n−k
C’est une variable d’espérance E(X) = nπ, et de variance V(x) = nπ(1−π).

012345
0
0.2
0.4
Valeurs k
Probabilités πk
Loi binomiale B(5, 0.2)
012 3 456789101112131415
0
0.2
0.4
Valeurs k
Probabilités πk
Loi binomiale B(25, 0.2)
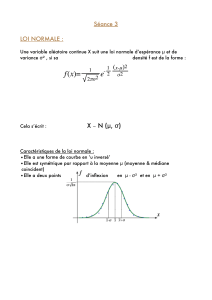
Définition 1.3 (Loi normale (Gaussienne) N(µ,σ))
C’est une variable aléatoire continue Xcaractérisée par une densité en forme de cloche, symétrique par
rapport à son espérance µet de variance σ2:
f(x) = 1
σ√2πe−(x−µ)2
2σ2.
−4−20246
0
0.1
0.2
0.3
0.4 N(0, 1)
N(1, 1.5)
Plusieurs remarques à son sujet :
— C’est la loi de probabilité limite obtenue à l’issue de népreuves de Bernouilli B(n,π)lorsque nπ
tend vers l’infini.
— Sa dispersion est telle que 95% des valeurs se trouvent dans l’intervalle [µ−1.96 σ;µ+1.96 σ].
— Toute combinaison linéaire Y=aX +bd’une variable aléatoire Gaussienne X∼ N(µ,σ)reste une
variable aléatoire Gaussienne d’espérance aµ+bet de variance a2σ2.
— En particulier, si X∼ N(µ,σ), alors X−µ
σsuit une loi normale centrée réduite N(0, 1).
Définition 1.4 (Loi de Student)
Soient deux variables aléatoires Xet Z, indépendantes l’une de l’autre, telles que Zsuit une loi normale
centrée réduite et Xune distribution du χ2àkdegrés de liberté, alors la variable aléatoire Tdéfinie par :
T=Z
√X/k
suit une loi de Student à kdegrés de liberté.

-4 -2 0 2 4
0.0 0.1 0.2 0.3 0.4
t
density
Gaussian
Student 1 df
Student 2 df
Student 5 df
— C’est en particulier le cas d’une variable aléatoire Gaussienne que l’on réduit non pas à l’aide de
l’écart-type théorique mais d’un écart-type estimé sur un échantillon.
— La courbe de la loi de Student ressemble à celle d’une loi Gaussienne, avec des queues de distribu-
tions plus épaisses.
— Plus le degré de liberté est grand, plus la courbe de la Student se rapproche de la courbe d’une loi
normale centrée réduite.
Définition 1.5 (Loi du χ2)
Soient kvariables aléatoires Gaussiennes indépendantes X1, . . . , Xk, alors la variable Xdéfinie par :
X=
k
∑
i=1
X2
i
suit une loi du χ2àkdegrés de liberté.
On remarque les propriétés suivantes :
—Xne prend que des valeurs positives ou nulles.
— La courbe de densité du χ2est asymétrique, avec une longue queue de distribution vers +∞.
— L’espérance de Xvaut ket sa variance 2k
Définition 1.6 (Loi de Fisher F(k1,k2))
Soient 2 variables aléatoires continues X1et X2indépendantes l’une de l’autre et distribuées chacune sui-
vant une loi du χ2à respectivement k1et k2degrés de liberté, alors la variable Fdéfinie par :
F=X1/k1
X2/k2
suit une loi de Fisher à k1et k2degrés de liberté. On remarque les propriétés suivantes :
— Si X∼ F(k1,k2), alors 1
X∼ F(k2,k1)
Définition 1.7 (Quantiles)
Pour appliquer les tests statistiques, on va souvent s’intéresser aux quantiles de la loi normale, d’une loi de
Student ou d’une loi du χ2tels qu’on peut les trouver dans les tables statistiques de ces distributions. Selon
les explications fournies avec les tables, on y lira :
— le quantile d’ordre α,qα, vérifiant :
P(X<qα) = α
C’est la valeur seuil telle que l’aire sous la courbe de densité située à gauche de qαsoit égale à α.
Cela signifie qu’il y a α% de chances pour que la variable Xsoit inférieure à qα. Il y a alors 1−α% de
chances pour que la variable Xsoit supérieure à qα.
qα
α

— l’opposé du quantile d’ordre α,dα, vérifiant :
P(X>dα) = α
C’est la valeur seuil telle que l’aire sous la courbe de densité située à droite de dαsoit égale à α. Cela
signifie qu’il y a α% de chances pour que la variable Xsoit supérieure à qα. Il y a alors 1−α% de
chances pour que la variable Xsoit inférieure à dα.
dα
α
Propriétés 1.1 (Opérations sur les variables aléatoires et changements d’échelle)
Soient deux variables aléatoires Xet Y.
1. De façon générale, E(X+Y) = E(X) + E(Y).
2. En particulier, l’espérance est linéaire, E(aX +b) = aE(X) + b.
3. Si Xet Ysont indépendantes l’une de l’autre, alors V(X+Y) = V(X) + V(Y).
4. V(aX +b) = a2V(X).
2 Estimation ponctuelle et intervalle de confiance
On s’intéresse à une variable aléatoire Xdont la distribution est caractérisée par un paramètre d’intérêt
inconnu θ. On étudie ce paramètre à l’aide d’un échantillon indépendamment et identiquement distribué de n
observations x1, . . . , xnde la variable X.
Définition 2.1 (Intervalle de confiance)
Un intervalle de confiance à (100 −α)% (on dit aussi au risque α) pour le paramètre θest un intervalle tel que
(100 −α)% des intervalles construits de la même manière à partir d’échantillons similaires indépendants
contiendront la vraie valeur du paramètre θ.
On observe un échantillon i.i.d. de taille n, noté (X1, . . . , Xn), d’une variable aléatoire Gaussienne Xdont
l’espérance µest inconnue, mais la variance σ2est connue :
X1, . . . , Xniid ∼ N(µ,σ2).
Définition 2.2 (Estimateur de l’espérance)
On estime l’espérance µpar la moyenne empirique :
M=1
n
n
∑
i=1
Xi
Lorsque la variance est inconnue, on l’estime à l’aide de l’estimateur sans biais de la variance.
Définition 2.3 (Estimateur non biaisé de la variance)
On estime la variance σ2par :
S2=1
n−1
n
∑
i=1
(Xi−M)2=1
n−1"n
∑
i=1
X2
i−nM2#
Lorsque l’on observe deux échantillons i.i.d. de deux variables aléatoires Gaussiennes X1et X2de tailles n1
et n2, de moyennes inconnues µ1et µ2et de même variance connue σ2:
X(i)
1, . . . , X(i)
niid
∼ N(µi,σ2),i=1, 2,
on utilise l’estimateur de la variance commune.

Définition 2.4 (Estimateur non biaisé de la variance commune)
On estime la variance commune σ2par :
S2=(n1−1)S2
1+ (n2−1)S2
2
n1+n2−2
Définition 2.5 (Intervalle de confiance d’une moyenne théorique)
IC1−α(µ) = "m±tn−1,α/2rs2
n#
Définition 2.6 (Intervalle de confiance d’une proportion théorique)
IC1−α(π) = "p±uα/2rp(1−p)
n#
3 Principes généraux sur les tests
Définition 3.1 (Erreur de type I ou Niveau d’un test)
C’est la probabilité de rejeter l’hypothèse nulle à tort, notée α:
α=P(Rejeter H0|H0est vraie)
Sous l’hypothèse H0
µ0u1−α/2 uα/2
Erreur de type I (α=5%)
Rejet de H0Rejet de H0
FIGURE 1 – Calibration d’un test sous H0
Définition 3.2 (Erreur de type II)
C’est la probabilité de ne pas rejeter l’hypothèse nulle, alors que l’on aurait dû, notée β:
β=P(Ne pas rejeter H0|H0est fausse)
Définition 3.3 (Puissance d’un test)
C’est la probabilité de rejeter l’hypothèse nulle à raison, c’est 1−β.