Ch. 07 Lois de Probabilité

Ch. 07 Lois de Probabilité
1
Ch. 07 Lois de Probabilité
I – LOI BINOMIALE
Définition
Une loi binomiale de paramètres n et p est notée B (n, p).
Son espérance mathématique est :
€
E(X)=np
.
Sa variance est :
€
V(X)=npq =np(1 −p)
.

Ch. 07 Lois de Probabilité
2
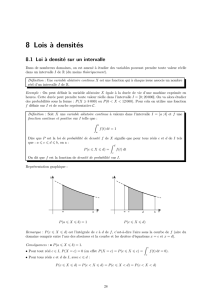
II – LOIS A DENSITE
A- loi continue
Approche
Dans le cas précédent, la variable aléatoire prend un nombre fini de valeurs.
Pour un grand nombre d’expériences aléatoires, les issues prennent pour valeur un nombre
quelconque situé dans un intervalle I de IR (exemples : le temps d’attente téléphonique à un service,
le taux d’alcoolémie …)
B- Densité sur un intervalle [ a ; b ]
Définition
On appelle fonction de densité sur un intervalle [a ; b], (a < b), toute fonction f définie, continue et
positive sur [a ; b] et telle que l’intégrale de cette fonction sur [a ; b] est égale à 1.
€
f(x)dx =1
a
b
∫
Exemple
Soit f la fonction continue et positive sur [0 ; 2] définie par
€
f(x)=x
2
. Montrer que f est une
fonction de densité sur [0 ; 2].
Définition
Soit X la variable aléatoire à valeurs dans [a ; b], munie d’une fonction de densité f.
On définit la loi de probabilité sur [a ; b] de densité f, en associant à tout intervalle [c ; d] inclus
dans [a ; b], la probabilité que X appartienne à l’intervalle [c ; d] :
€
P(X∈[c ; d]) =P(c≤x≤d)=f(x)dx
c
d
∫
.
Propriétés
• Pour tout nombre réel c de [a ; b],
€
P({c}) =0
.
• Pour tout nombre réel c de [a ; b],
€
P(X∈[c ; b]) =1−P(X∈[a ; c])

Ch. 07 Lois de Probabilité
3
C- Loi uniforme sur un intervalle [ a ; b ]
Définition et conséquences
On dit qu’une variable aléatoire X suit une loi uniforme sur [a ; b], lorsque sa densité est constante
sur [a ; b].
La fonction de densité f de la loi uniforme sur l’intervalle [a ; b] est définie par
€
f(x)=1
b−a
.
Propriétés
• Pour tout intervalle [c ; d] de [a ; b], on en déduit :
€
P(X∈[c ; d]) =1
b−a
dx =d−c
b−a
c
d
∫
.
• L’espérance de la loi uniforme sur [a ; b] est définie par :
€
E(X)=x f(x)dx =1
b−ax dx
a
b
∫
a
b
∫=1
b−a
b2
2−a2 2
$
%
&
'
(
) =a+b
2
.
III – LOI NORMALE N (0 ; 1)
Approche d’une densité par la loi binomiale
Une variable aléatoire X suit une loi binomiale B(n ; p), d’espérance
€
µ =np
et d’écart type
€
σ =npq =np(1 −p)
, avec 0 < p < 1.
Soit la variable aléatoire
€
Z=X−
µ
σ
, alors
€
P(a≤X≤b)=P(c≤Z≤d)
, où
€
c=a−
µ
σ
et
€
d=b−
µ
σ
.

Ch. 07 Lois de Probabilité
4
Définition
Une variable aléatoire X, d’espérance µ = 0 et d’écart type σ=1, suit la loi normale centrée réduite,
notée N (0 ; 1) lorsqu’elle admet pour fonction de densité la fonction f définie sur IR par :
€
f(x)=1
2 π
e−x2
2
.
Propriétés
(1) f est continue sur IR.
(2) Pour tous nombres réels a et b,
€
P(a≤X≤b)=f(x)dx
a
b
∫
.
(3) L’aire totale sous la courbe est égale à
1 ; elle représente la probabilité
€
P(X∈−∞ ; +∞
] [
)
.
(4) La courbe de f est symétrique par
rapport à l’axe des ordonnées, donc
€
P(X∈0 ; +∞
[ [
)=1
2
.
On dit que la courbe de f est une
courbe en cloche.
(5) Pour tout nombre réel u :
€
P(X≤ −u)=1−P(X>−u)
, or pour
des raisons de symétrie
€
P(X>−u)=P(X≤u)
donc
€
P(X≤ −u)=1−P(X≤u)
.
(6) Cas particuliers : avec la calculatrice,
on obtient :
€
P(X∈[−1 ; 1]) ≈0,68.
€
P(X∈[−1,96 ; 1,96]) ≈0,95.
€
P(X∈[−2 ; 2]) ≈0,954.
€
P(X∈[−3 ; 3]) ≈0,997.

Ch. 07 Lois de Probabilité
5
IV – LOI NORMALE N (µ ; σ2)
A- Loi Normale
Définition
Une variable aléatoire X suit la loi normale N (µ ; σ2) lorsque la variable aléatoire
€
T=X−
µ
σ
suit la
loi normale N (0 ; 1).
Propriétés
Si la variable aléatoire X suit la loi normale N (µ ; σ2) alors son espérance est
€
E(X)= µ
et son écart
type est σ.
Remarque
Si la variable aléatoire X suit la loi normale N (µ ; σ2) alors la fonction F définie sur IR par
€
F(x)=P(X≤x)
est strictement croissante sur IR. De plus,
€
F( µ )=P(X≤ µ )=0,5
.
B- Critères de normalité
Définition
Si la variable aléatoire X suit la loi normale N (µ ; σ2) alors :
☞
€
P(X∈[ µ − σ ; µ + σ ]) ≈0,68
☞
€
P(X∈[ µ −2 σ ; µ +2 σ ]) ≈0,954
☞
€
P(X∈[ µ −3 σ ; µ +3 σ ]) ≈0,997