Chapitre VIII - Complexes (Partie II) 9 Notation exponentielle de la

Chapitre VIII - Complexes (Partie II)
9 Notation exponentielle de la forme trigonométrique
Définition 1. Tout nombre complexe znon nul peut s’écrire sous la forme :
z=reiθ où r=|z|et θ=arg z[2 π]
Cette écriture est appelée forme exponentielle de z.
Remarque. •Pour tout rréel positif non nul et θréel, z=reiθ =r(cos θ+ i sin θ)
•eiθ est le nombre complexe de module 1 et dont un argument est θ.
Pour tout réel θ,eiθ =cos θ+ i sin θ
•ei0= 1 eiπ
2= i eiπ =−1e−iπ 2=−i
•z=−2 eiπ
3n’est pas écrit sous forme exponentielle (car −2<0)
mais z= eiπ ×2 eiπ
3= 2 eiπ+π
3= 2 ei4π
3est sous forme exponentielle.
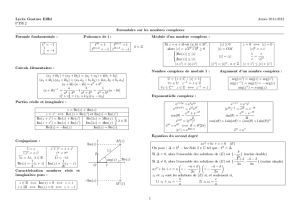
•On retrouve les propositions 9 et 10.
Soit z=reiθ et z′=r′eiθ ′deux nombres complexes non nuls, r > 0,r′>0et n∈N.
1. z¯ = re−iθ avec |z¯|=ret arg (z¯) = −θ[2π]
2. −z=rei(θ+π)avec |−z|=ret arg (−z) = θ+π[2π]
3. z z ′=reiθ ×r′ei θ ′=r r′ei(θ+θ′)avec |z z ′|=r r′et arg (z z ′) = θ+θ′[2π]
4. zn= (reiθ)n=rneinθ avec |zn|=rnet arg (zn) = n θ [2π]
5. z
z′=reiθ
r′eiθ ′=r
r′ei(θ−θ′)avec 
z
z′
=r
r′et argz
z′=θ−θ′[2π]
v
Ou
ei0
eiπ
2
eiπ
e−iπ
2
z=reiθ
z¯ = re−iθ
−z=rei(θ+π)
Exemple 1. Écrire sous forme algébrique les nombres complexes : z1= 3 e2i π
3;z2= 2 e−iπ;z3=eiπ
2 eiπ
4
.
•z1= 3cos 2π
3+ i sin 2π
3= 3 −1
2+ i 3
√
2!=−3
2+ i 3 3
√
2•z2= 2 ×(−1) = −2
•z3=eiπ
2 eiπ
4
=1
2eiπ−
π
4=1
2ei3π
4=1
2cos 3π
4+ i sin 3π
4=1
2 −2
√
2+ i 2
√
2!=−2
√
4+ i 2
√
4
Exemple 2. Écrire sous forme exponentielle les nombres complexes : z1=−3 + 3 i 3
√;z3=3
√−i
2 i et z4= (1 + i)5.
• |z1|= (−3)2+3 3
√2
q=36
√= 6 donc z1= 6 −3
6+ i 3 3
√
6!= 6 −1
2+ i 3
√
2!= 6cos 2π
3+ i sin 2π
3=6 ei2π
3
•3
√−i = 2 3
√
2−i1
2!= 2 e
−iπ
6et 2 i = 2 eiπ
2donc z3=3
√−i
2 i =2 e
−iπ
6
2 eiπ
2
= ei−
π
6
−
π
2= e
−4i π
6=e
−i2π
3z3est un quotient de nombres complexes
•1 + i = 2
√ 2
√
2+ i 2
√
2!= 2
√eiπ
4donc z4= (1 + i)5=2
√eiπ
45
= 2
√5ei5π
4=4 2
√ei5π
4z4est une puissance de nombre complexe
Exemple 3. Soit z= 3 eiπ
3. Montrer que z57 est un nombre réel. Préciser son signe.
arg (z57) = 57 arg z=57 π
3=19 π= 9 ×2π+π[2 π]soit arg (z57) = π[2 π].
De plus, 3>0, donc z57 est un nombre réel négatif .On a plus précisément : z57 = 357 eiπ=−357
Exemple 4. Soit A,Bet Ctrois points du plan complexe d’affixes respectives : zA= 2
√eiπ
4;zB= 4 + 2 i et zC=−5−i. Montrer que A,Bet Calignés.
zA= 2
√eiπ
4= 2
√ 2
√
2+ i 2
√
2!= 1 + i donc zA B =zB−zA= 4 + 2 i −(1 + i) = 3 + i et zA C =zC−zA= (−5−i) −(1 + i) = −6−2 i =−2 (3 + i)
zA C =−2zA B donc les points A,Bet Csont alignés.
Exemple 5. Soit A,Bet Cd’affixes : zA=−2 i ;zB=−3
√+ i et zC= 3 √+ i. Mettre zB−zA
zC−zA
sous forme exponentielle, en déduire la nature de A B C.
•zB−zA
zC−zA
=−3
√+ i + 2 i
3
√+ i + 2 i =−3
√+ 3 i
3
√+ 3 i =3 2
√ei2π
3
3 2
√eiπ
3
= e
i2π
3
−
π
3=eiπ
3de module 1 et d’argument π
3[2 π]
•
zB−zA
zC−zA
=AB
AC = 1 soit AB =AC et arg
zB−zA
zC−zA=arg(zB−zA)−arg(zC−zA) = A C ;A B =π
3[2 π]
donc ABC est un triangle équilatéral car c’est un triangle isocèle dont l’angle au sommet est égal à π
3.
Proposition 1. Formule de Moivre Pour tout réel θet tout entier naturel n,
(eiθ)n= ein θ soit (cos θ+ i sin θ)n=cos (n θ) + i sin (n θ)
Proposition 2. Formules d’Euler Pour tout réel θ,cos θ=eiθ+ e−iθ
2et sin θ=eiθ−e−iθ 2 i
Démonstration. Pour tout réel θ,eiθ =cos θ+ i sin θet e−iθ =cos θ−isin θ. Sommer et soustraire membre à membre puis conclure. 