BAC BLANC

BAC BLANC
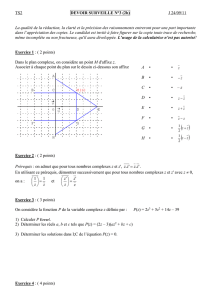
Exercice 1 : 6 points
Partie 1 : Etude d’une fonction f
On appelle f la fonction définie sur l’intervalle I=]-
1;
2
+ ∞
[ par f(x)=ln(1+2x)
1. Justifier que f est strictement croissante sur l’intervalle I
2. Déterminer la limite de f(x) quand x tend vers
1
2
−
3. On considère la fonction g définie sur l’intervalle I par g(x)= f(x)-x
a. Etudier les variations de g sur l’intervalle I
b. Justifier que l’équation g(x)=0 admet deux solutions 0 et une autre, notée β,
appartenant à l’intervalle [1 ; 2]
c. En déduire le signe de g(x) pour x appartenant à l’intervalle I
4. Justifier que, pour tout réel x appartenant à l’intervalle ]0 ;β[, f(x) appartient aussi à
]0 ;β[
Partie 2 : Etude d’une suite récurrente
On appelle
( )
0
nn
U
≥
, la suite définie par
1 0
( ) et 1
n n
U f U U
+
= =
1. Démontrer par récurrence que, pour tout entier naturel n ,
n
U
appartient à
l’intervalle ]0 ;β[
2. Démontrer par récurrence que la suite
( )
0
nn
U
≥
est croissante
3. Justifier que la suite
( )
0
nn
U
≥
est convergente et déterminer sa limite

Exercice 2 : 5 points
Pour les élèves ne faisant pas spécialité
Le plan est muni d’un repère orthonormal direct
( )
; ;O u v
r r
( unité graphique 1cm)
Soient A B et I les points d’affixes respectives 1+i, 3-i et 2
A tout point M d’affixe z, on associe le point M’ d’affixe z’ telle que z’=z²-4z. Le point M’
est appelé image de M
1. Faire une figure et compléter cette figure tout au long de l’exercice
2. Calculer les affixes des points A’ et B’, images respectives des points A et B. Que
remarque-t-on ?
3. Déterminer les points qui ont pour image le point d’affixe -5
4. a. Vérifier que, pour tout nombre complexe z, on a z’+4 = (z-2)²
b. En déduire une relation entre |z’+4|`et |z-2| et, lorsque z est différent de 2, une
relation entre arg(z’+4) et arg(z-2)
c. Que peut-on dire du point M’ lorsque M décrit le cercle C de centre I et de rayon 2
5. Soient E le point d’affixe
3
2 2
i
e
π
+
, J le point d’affixe -4 et E’ l’image de E
a. Calculer la distance IE et une mesure en radians de l’angle
( )
;u IE
r uur
b. Calculer la distance JE’ et une mesure en radians de l’angle
( )
; 'u JE
r uuur
c. Construire à la règle et au compas le point E’ ; on laissera apparents les traits
de construction

Exercice 2 : 5 points
Pour les élèves faisant spécialité
Le plan est muni d’un repère orthonormal direct
( )
; ;O u v
r r
Soient A et B les points d’affixes respectives
7
1 et 7 2
A B
z i z i = − = +
1. On considère la droite (d) d’équation 4x+3y=1. Démontrer que l’ensemble des
points de (d) dont les coordonnées sont entières est l’ensemble des points
( )
3 1; 4 1
k
M k k + − −
lorsque k décrit l’ensemble des entiers relatifs
2. Déterminer l’angle et le rapport de la similitude directe de centre A qui
transforme B en
( )
1
2;3M
−
−
3. Soit s la transformation du plan qui, à tout point M d’affixe z, associe le point
M’ d’affixe
2 1 5
'3 3 3 z iz i = + −
. Déterminer l’image de A par s puis donner la
nature et les éléments caractéristiques de s
4. On donne
1
B
l’image de B par s et , pour tout entier naturel non nul,
1
l'image de
n n
B B
+
par s
a. Déterminer la longueur
1
en fonction de
n n
AB AB
+
b. A partir de quel entier n le point
n
B
appartient-il au disque de centre A et de rayon
2
10
−
c. Déterminer l’ensemble des entiers n pour lesquels
1
, et
n
A B B
sont alignés

Exercice 3 : 4 points
On considère dans l’espace un cube de 3cm de côté, noté ABCDEFGH.
Soit I le barycentre des points pondérés (E ;2) et (F ;1), J celui de (F ;1) et (B ;2) et K celui de
(G ;2) et (C ;1)
On veut déterminer l’ensemble des points M équidistants de I, J et K. On note Δ cet ensemble.
1. Placer les points I, J et K sur le cube
2. Soit Ω le point de Δ situé dans le plan (IJK). Que représente ce point pour le triangle
IJK ?
Pour la suite de l’exercice, on se place maintenant dans le repère orthonormal suivant
1 1 1
; ; ;
3 3 3
A AD AB AE
uuur uuur uuur
3. Donner les coordonnées des points I, J et K
4. Soit P(2 ;0 ;0) et Q(1 ;3 ;3) deux points qu’on placera sur la figure. Démontrer que la
droite (PQ) est orthogonale au plan (IJK)
5. Soit M un point de l’espace de coordonnées (x ;y ;z)
a. Démontrer que M appartient à l'ensemble Δ si et seulement si le triplet (x ;y ;z) est
solution de deux équations linéaires que l’on écrira. Quelle est la nature de Δ ?
b. Vérifier que P et Q appartiennent à Δ
6. a. Déterminer un vecteur normal au plan (IJK) et en déduire une équation cartésienne
de ce plan
b. Déterminer les coordonnées exactes de Ω

Exercice 4 : 2,5 points
Un chariot de masse 200kg se déplace sur une voie rectiligne et horizontale. Il est soumis
à une force d’entraînement constante
F
ur
de valeur 50N. Les forces de frottement sont
proportionnelles à la vitesse et de sens contraire ; le coefficient de proportionnalité a pour
valeur absolue 25 N.m-1.s-1
La position du chariot est repérée par la distance x, en mètres, du point H à l’origine O du
repère en fonction du temps t, exprime en secondes. On prendra t dans l’intervalle [0 ;+∞[.
Les lois de Newton conduisent à l’équation différentielle (E) : 25x’+200x’’= 50 où x’ est la
dérivée de x par rapport au temps t et x’’ est la dérivée seconde de x par rapport à t.
1. On note v(t) la vitesse du chariot au temps t, on rappelle que v(t)=x’(t).
Prouver que x est solution de (E) si et seulement si x’ est solution de l’équation
différentielle (F) :
1 1
'8 4 v v = − +
.
Résoudre l’équation différentielle (F)
2. On suppose que, à l’instant t=0, on a : x(0)=0 et x’(0)=0
a. Calculer pour tout nombre réel positif t, x’(t)
b. En déduire que l’on a, pour tout nombre réel positif t ,
8
( ) 2 16 16
t
x t t e
−
= − +
3. On note
lim ( )
t
V v t
→ + ∞
=
. Pour quelles valeurs de t la vitesse du chariot est-elle
inférieure ou égale à 90% de sa valeur limite V ?
4. Quelle est la distance parcourue par le chariot au bout de 30 secondes ? On
exprimera cette distance en mètres, au décimètre près