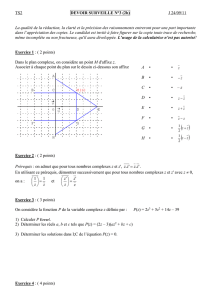
Exercice 2 ( 5 points )

BACCALAURÉAT (BLANC) GÉNÉRAL
Lycée Joseph LOTH
Session mai 2013
MATHÉMATIQUES
– Série S –
ENSEIGNEMENT OBLIGATOIRE
Durée de l’épreuve : 4 heures
Les calculatrices électroniques de poche sont autorisées,
conformément à la réglementation en vigueur.
Le sujet est composé de 4 exercices indépendants. Le candidat doit traiter tous les exercices. Dans
chaque exercice, le candidat peut admettre un résultat précédemment donné dans le texte pour
aborder les questions suivantes, à condition de l’indiquer clairement sur la copie.
La qualité de la rédaction, la clarté et la précision des raisonnements
entreront pour une part importante dans l’appréciation des copies.
Avant de composer, Le candidat s’assurera que le sujet comporte bien 6 pages numérotées de 1 à 6
Page 1/6

EXERCICE 1 ( 5 points )
(Commun à tous les candidats)
Le plan complexe est rapporté à un repère orthonormal direct
( ; , )O u v
. L’unité graphique est 1 cm.
On désigne par A, B et C les points d’affixes respectives
23
A
zi
,
B
zi
et
6
C
zi
.
On réalisera une figure que l’on complétera au fur et à mesure des questions.
Partie A
1. Calculer
BA
CA
zz
zz
.
2. En déduire la nature du triangle ABC .
Partie B
On considère l’application f qui, à tout point M d’affixe z distincte de i , associe le point
M'
d’affixe
z'
telle que :
23i z i
z' zi
.
1. Soit D le point d’affixe
1
D
zi
. Déterminer l’affixe du point
D'
image du point D par f.
2. a. Montrer qu’il existe un unique point, noté E, dont l’image par l’application f est le point d’affixe 2 i .
b. Démontrer que E est un point de la droite (AB).
3. Démontrer que, pour tout point M distinct du point B,
'AM OM BM
.
4. Démontrer que, pour tout point M distinct du point A et du point B, on a l’égalité :
; ' ; 2
2
u OM BM AM k
,
k
.
5. Démontrer que si le point M appartient à la médiatrice du segment [AB] alors le point
M'
appartient
à un cercle dont on précisera le centre et le rayon.
6. Démontrer que si le point
M'
appartient à l’axe des imaginaires purs, privé du point B, alors le point
M appartient à la droite (AB).
Page 2/6

EXERCICE 2 ( 5 points )
(Pour les candidats ne passant pas la Spécialité Mathématiques)
Le plan est muni d’un repère orthonormal.
;,O i j
d’unité 1 cm.
Soit f la fonction définie par
2
( ) .cos
x
f x e x
représentée ci-dessous.
Soit C cette courbe représentative.
1. Montrer que pour tout réel x, on a
21
( ) . cos sin
2
x
f x e x x
.
2. a. Résoudre dans l’équation f (x)=0.
b. Montrer que sur
,
22
, on a
( ) 0fx
.
c. Montrer que pour tout réel x, (E) :
4 ( ) 4 ( ) 5 ( )f x f x f x
.
3. Soit l’intégrale
/2
/2
()I f x dx
.
On considère la fonction F telle que, pour tout réel x,
1
( ) 4 ( ) 4 ( )
5
F x f x f x
.
a. Sachant que f vérifie (E), montrer que F est une primitive de f.
b. Etablir que
44
5 2 2 5 2 2
I f f f f
puis que
44
4
5
I e e
c. Interpréter graphiquement ce résultat.
Page 3/6
x
y
-4 -2 0 2 4 6 8
-4
-2
0

Exercice 3 ( 6 POINTS )
(Commun à tous les candidats)
Partie A
On considère la fonction f définie et dérivable sur l’intervalle
0;
par
5ln 3f x x x  
.
1. a. On appelle
f
la fonction dérivée de la fonction f sur
0;
.
Calculer
fx
et étudier son signe sur
0;
.
b. Donner, dans un tableau, les variations de f sur l’intervalle
0;
.
c. Montrer que, pour tout x strictement positif on a
ln 3
5 1 5ln 1
x
f x x xx
.
d. En déduire la limite de f en .
e. Compléter le tableau de variation de f sur l’intervalle
0;
.
2. a. Montrer que l’équation
( ) 0fx
admet une unique solution dans l’intervalle
0;
.
On notera cette solution.
b. Après avoir vérifié que appartient à l’intervalle [14 ; 15], donner une valeur approchée de
à 10–2 près.
c. En déduire le signe de f sur l’intervalle
0;
.
Partie B
Soit
n
u
la suite définie par
0
1
45ln 3
n
n
u
uu
pour tout entier naturel
0n
.
On considère la fonction g définie sur l’intervalle
0;
par
5ln 3g x x
.
Sur le document en annexe (page6/6), on a tracé dans un repère orthonormé la droite D d’équation
y = x et la courbe C, courbe représentative de la fonction g.
1. a. Construire sur l’axe des abscisses de la figure les termes
0
u
,
1
u
,
2
u
de la suite
n
u
en utilisant
la droite et la courbe données et en laissant apparents les traits de construction.
b. Formuler une conjecture sur le sens de variations de la suite
n
u
.
2. a. Étudier le sens de variations de la fonction g sur l’intervalle
0;
.
b. Vérifier que
g
où est défini dans la partie A question 2. a.
c. Démontrer par récurrence que, pour tout entier naturel n, on a
0n u
.
d. Démontrer alors la conjecture émise à la question 1. b. de la partie B.
e. En utilisant la question 2. a. de la partie A, justifier que
lim
nn
u
.
3. On considère l’algorithme suivant :
u prend la valeur 4
Répéter Tant que u − 14,2 < 0
u prend la valeur de 5ln(u + 3)
Fin du Tant que
Afficher u
a. Justifier que cet algorithme se termine.
b. Donner la valeur que cet algorithme affiche (on arrondira à 3 décimales).
Page 4/6

Exercice 4 ( 4 POINTS )
(Commun à tous les candidats)
Cet exercice est un QCM qui comporte 8 questions, numérotées de 1 à 8. À chaque question, une seule des
réponses est exacte. Si vous décidez de répondre, vous reporterez clairement sur la copie le numéro de la
question et la réponse COMPLETE choisie. Aucune justification n’est demandée.
Barème : une réponse exacte rapporte 0,5 point. Une réponse fausse ou une absence de réponse n’enlèvent pas
de point.
Partie A - Géométrie
Dans l’espace rapporté à un repère orthonormal les points :
A(1, 0, 0), B(1, 1, 0), C(1, 2, 0), D(1, 0, 1), E(1, 1, 1), F(1, 2, 1),
G(0, 0, 1),H(0, 1, 1), I(0, 2, 1), J(O, 1, 0), K(0, 2, 0)
comme indiqués sur la figure ci -contre :
1. Le triangle GBI est :
a) isocèle. b) équilatéral. c) rectangle.
2. Les points B, C, I, H :
a) sont non coplanaires. b) forment un rectangle. c) forment un carré.
3. Une représentation paramétrique de paramètre t de la droite (KE) est :
a)
2,
xt
y t t
zt
b)
34
,
4
xt
y t t
zt
c)
1
1,
1
xt
y t t
zt
4. Le volume du tétraèdre HJKB est égal à :
a)
1
2
b)
1
6
c)
1
3
Partie B – Probabilités.
5. Soit A et B deux évènements indépendants d’un même univers tels que
( ) 0,3pA
et
( ) 0,65p A B
.
La probabilité de l’événement B est :
a) 0,5 b) 0,35 c) 0,46 d) 0,7
6. On suppose que la durée d’attente à un guichet de service, exprimée en heure, suit la loi uniforme
sur l’intervalle [0 ;1]. La probabilité que la durée d’attente d’une personne prise au hasard soit
comprise entre 15 min et 20 min est :
a)
1
3
b)
1
5
c)
1
12
d)
1
4
.
(suite du QCM page suivante)
Page 5/6