Cabinet de recrutement

France-Examen 2012 Tous droits réservés Reproduction sur support électronique interdite page 1/5
RAPPEL DU SUJET
EXERCICE 2 (5 points)
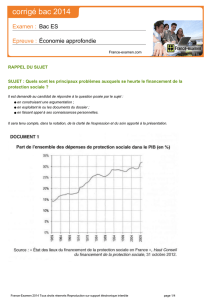
Pour embaucher ses cadres une entreprise fait appel à un cabinet de recrutement. La procédure retenue est la
suivante. Le cabinet effectue une première sélection de candidats sur dossier. 40% des dossiers reçus sont validés et
transmis à l'entreprise. Les candidats ainsi sélectionnés passent un premier entretien à l'issue duquel 70% d'entre eux
sont retenus. Ces derniers sont convoqués à un ultime entretien avec le directeur des ressources humaines qui
recrutera 25% des candidats rencontrés.
1. On choisit au hasard le dossier d'un candidat.
On considère mes évènements suivants :
a. Reproduire et compléter l'arbre pondéré ci-dessous.
b. Calculer la probabilité de l'évènement
c. On note F l'événement "Le candidat n'est pas recruté".
Démontrer que la probabilité de l'événement F est égale à 0,93
© France-Examen – 2012 Tous droits réservés – Reproduction sur support électronique interdite page 1/5
corrigé bac 2012
Examen : Bac S
Epreuve : Mathématiques
France-examen.com

France-Examen 2012 Tous droits réservés Reproduction sur support électronique interdite page 2/5
2. Cinq amis postulent à un emploi de cadre dans cette entreprise. Les études de leur dossier sont faites
indépendammment les unes des autres. On admet que la probabilité que chacun d'eux soit recruté est égale à 0,07.
On désigne par X la variable aléatoire donnant le nombre de personnes recrutées parmi ces cinq candidats.
a. Justifier que X suit une loi binomiale et préciser les paramètres de cette loi.
b. Calculer la probabilité que deux exactement des cinq amis soient recrutés. On arrondira à .
3. Quel est le nombre minimum de dossiers que le cabinet de recrutement doit traiter pour que la probabilité
d'embaucher au moins un candidat soit supérieure à 0,999 ?
LE CORRIGÉ
I. INTERET DU SUJET
Utiliser un arbre pondéré pour traduire des probabilités conditionnelles et utilisation de la loi binomiale
II. SAVOIRS ET SAVOIRS FAIRE
●Arbre pondéré
●Probabilités conditionnelles
●Loi binomiale
●Fonction logarithme
© France-Examen – 2012 Tous droits réservés – Reproduction sur support électronique interdite page 2/5
corrigé bac 2012
Examen : Bac S
Epreuve : Mathématiques
France-examen.com

France-Examen 2012 Tous droits réservés Reproduction sur support électronique interdite page 3/5
III. REPONSES
1) a)
2) a) Loi binomiale : 5 épreuves indépendantes binaires
3) n= 96
© France-Examen – 2012 Tous droits réservés – Reproduction sur support électronique interdite page 3/5
corrigé bac 2012
Examen : Bac S
Epreuve : Mathématiques
France-examen.com

France-Examen 2012 Tous droits réservés Reproduction sur support électronique interdite page 4/5
IV DEVELOPPEMENT
1) a)
b)
2) a) Comme on est en présence de cinq épreuves indépendants présentant chacune deux issues, soit la personne est
recrutée avec une probabilité p=0,07 soit elle ne l'est pas avec une probabilité q=0,93. Par conséquent la variable
aléatoire X donnant le nombre k de personnes recrutées parmi ces cinq candidats, suit une loi binomiale de paramètres
n=5 et p=0,07.
© France-Examen – 2012 Tous droits réservés – Reproduction sur support électronique interdite page 4/5
corrigé bac 2012
Examen : Bac S
Epreuve : Mathématiques
France-examen.com

France-Examen 2012 Tous droits réservés Reproduction sur support électronique interdite page 5/5
Le cabinet doit donc traiter au minimum 96 dossiers pour que la probabilité d'embaucher au moins un candidat soit
supérieure à 0,999.
L'AVIS DU PROF
Il fallait penser aux propriétés des logarithmes pour déterminer le nombre minimal de dossiers à étudier.
© France-Examen – 2012 Tous droits réservés – Reproduction sur support électronique interdite page 5/5
corrigé bac 2012
Examen : Bac S
Epreuve : Mathématiques
France-examen.com