Angles inscrits

Angles et cercles
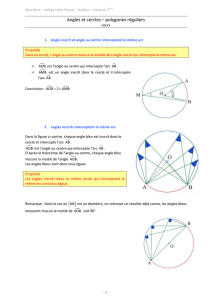
Hypothèses
Cest un cercle de centre Oet de rayon R.
A,Bet Msont trois points de C.
mest le point diamétralement opposé à M.
Vocabulaire
Le segment AB est une corde de C.
Les points Aet Bdéfinissent sur Cdeux arcs de cercle d’extré-
mités Aet B:
1. l’arc saillant AB, correspondant au chemin le plus court
entre Aet B;
2. l’arc rentrant AB, correspondant au chemin le plus long
entre Aet B.
x
360 x
O
B
A
M
m
De même, Aet Bpermettent de définir deux angles de même sommet O:
1. l’angle saillant AOB (c’est l’angle habituel, dont la mesure xest comprise entre 0 et 180 ;
2. l’angle rentrant AOB (c’est l’angle dont la mesure est 360 x).
On dit que AOB est l’angle au centre interceptant l’arc AB et que AOB est l’angle au centre interceptant
l’arc AB.
AM B est un angle inscrit interceptant l’arc AB.
AmB est un angle inscrit interceptant l’arc AB.
Remarque – Lorsque Aet Bsont diamétralement opposés, la longueur de AB est égale à la longueur de AB
et les angles AOB et AOB ont la même mesure : 180 .
Objectif : Comparer les angles AOB et AM B, en fonction de la position du point Msur C.
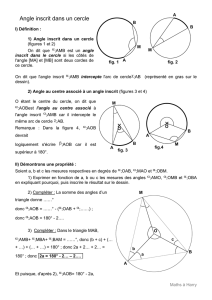
Quelques questions préliminaires
1. Quelle est la nature du triangle mAM ? Qu’en déduit pour la somme des mesures des angles AmO et
AM O ?
2. Quelle est la nature du triangle OAM ? Qu’en déduit-on pour les angles OAM et AM O ?
3. Comparer les mesures des angles mAO et AmO.
3 MF2 Angles et cercles Page 1/3

I – Met Osont dans le même demi-plan de frontière AB 1
Cas n˚1 : Oest à l’intérieur du triangle AM B.
1. Prouver que AOm 2AM m.
2. Quelle relation analogue peut-on écrire entre mOB et mM B.
3. En déduire une relation entre AOB et AM B.
O
B
A
M
m
Cas n˚2 : Oest à l’extérieur du triangle AM B.
Prouver qu’on a encore AOB 2AM B.
A
M
m
B
O
II – Met Osont de part et d’autre de la droite AB .
Prouver que 2AM B AOB.
A
M
m
B
O
1. Cela signifie que que Met Osont du même côté de la droite AB .
3 MF2 Angles et cercles Page 2/3

III – Comparaison d’angles inscrits.
En utilisant les résultats précédemment établis :
1. Comparer AM B et AN B.
2. Comparer AM B et AP B.
A
M
B
N
P
Compléter et apprendre la synthèse suivante :
Synthèse :
1. Si dans un cercle, un angle inscrit et un angle au centre intercepte le même arc de cercle, alors . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Si dans un cercle, deux angles inscrits interceptent le même arc de cercle, alors . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 MF2 Angles et cercles Page 3/3