Angles et polygones réguliers

Angles et polygones réguliers
1) Angle inscrit – Angle au centre
A) Définitions
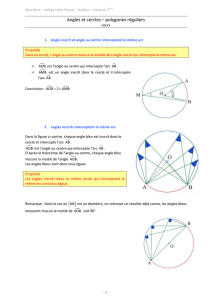
Exemple :
En mesurant, on constate que : A;J1B = A ;J2B = A ;J3B = 46° et ;AOB = 92°
Définition d’un angle inscrit :
Un angle inscrit est formé par deux cordes issues d’un même point du cercle
Exemple :
A;J1B, A ;J2B et A ;J3B sont des angles inscrits interceptant l’arc AB.
Définition d’un angle au centre :
Un angle au centre est un angle dont le sommet est au centre du cercle.
Exemple :
;AOB est un angle au centre interceptant l’arc AB.
B) Propriétés
Propriété 1 :
La mesure d’un angle au centre est le double de celle de l’angle inscrit qui intercepte le même arc.
Propriété 2 :
Deux angles inscrits qui interceptent le même arc ont la même mesure.

1) 2)
Remarque :
Si l’angle au centre est plat (180°), alors un angle inscrit interceptant le même arc mesure 180 : 2 = 90°
On retrouve le théorème du triangle rectangle inscrit vu en 4e.
2) Polygone régulier
Définition :
Un polygone régulier est un polygone inscrit dans un cercle dont tous les côtés ont la même longueur et dont
tous les angles ont la même mesure.
Propriété :
L’angle au centre d’un polygone a n côtés, de centre O et dont les points A et B sont deux côtés consécutifs a
pour mesure : AOB =
n360
Exemples :