Cours de mathématiques de première S

Chapitre 3Dérivation des fonctions
3.1 Généralités
3.1.1 Limite en 0
Définition 3.1 Soit f une fonction définie sur un intervalle I contenant 0et L ∈R.
On dit que f (x)tend vers L quand x tend vers 0(ou que L est la limite de f(x)quand x tend vers
0) si on peut rendre f (x)aussi proche de L que l’on veut pour x suffisamment proche de 0. On
note : lim
x→0f(x)=L
Exemple lim
x→0x2=0 lim x→0x+1=1 lim x→0px+x−2=−2...
Exemple Déterminer la limite en 0 de x2−2x
3x.
Pour tout x6=0, x2−2x
3x=x−2 3donc lim
x→0
x2−2x
3x=−2 3.
3.1.2 Nombre dérivé
Définition 3.2 Soit f une fonction définie sur un intervalle I. Soit a ∈I et h 6=0tel que a+h∈I.
On appelle taux de variation de f entre a et a +h le réel f(a+h)−f(a)
h.
On dit que f est dérivable en a si, lorsque h tend vers 0, le taux de variation de f entre a et a +h
tend vers un réel L autrement dit si lim
h→0
f(a+h)−f(a)
h=L.
Ce réel L est appelé nombre dérivé de f en a et se note f 0(a).
Exemple Démontrer que la fonction f :x7−→ x2est dérivable en 2 et calculer f 0(2).
Démontrer que la fonction g :x7−→px n’est pas dérivable en 0.
– Pour tout h6=0, f(2+h)−f(2)
h=(2+h)2−4 h=h2+4h h=h+4
Ainsi lim
h→0
f(2+h)−f(2)
h=4.
fest donc dérivable en 2 et f0(2) =4.
– Pour tout h6=0, g(0+h)−g(0)
h=ph h=1
ph.
Or, 1
phn’a pas de limite finie lorsque htend vers 0 donc gn’est pas dérivable en 0.
Première S4 – 2016/2017 15

DÉRIVATION DES FONCTIONS COURS
3.1.3 Interprétation graphique
Théorème 3.1
Soit fune fonction définie sur Iet Cfsa représentation graphique dans un repère. Soit a∈I.
Si fest dérivable en aalors f0(a) est le coefficient directeur de la tangente à Cfau point
A(a;f(a)). L’équation de cette tangente est alors : y=f0(a)(x−a)+f(a).
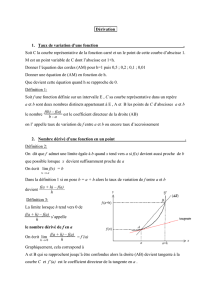
Illustration : Soit A(a;f(a)) ∈Cf.
Soit h6=0 et M(a+h;f(a+h)) ∈Cf.
Le quotient f(a+h)−f(a)
hreprésente le coefficient
directeur de la droite (AM). Lorsque htend vers 0,
Mse rapproche de Aet la droite (AM) tend à se
confondre avec la tangente à Cfen A.
a
f(a)
a+h
f(a+h)
DÉMONSTRATION
Soit Tla tangente à la courbe au point A. Son coefficient directeur est f0(a) donc l’équation réduite
de Test de la forme y=f0(a)x+b.
A∈Tdonc f(a)=f0(a)a+bdonc b=f(a)−a f 0(a).
L’équation de Test donc y=f0(a)x+f(a)−a f 0(a) soit y=f0(a)(x−a)+f(a).
3.2 Calculs de dérivées
3.2.1 Fonction dérivée
Définition 3.3 Soit f une fonction définie sur un intervalle I.
– Si, pour tout x de I, f est dérivable en x, on dit que f est dérivable sur I.
– La fonction définie sur I par x 7−→ f0(x)est appelée fonction dérivée de f . Cette fonction est
notée f 0.
3.2.2 Dérivées usuelles
Fonctions constantes
Théorème 3.2
Si fest la fonction définie sur Rpar : f(x)=k
alors fest dérivable sur Ret pour tout réel x:f0(x)=0.
DÉMONSTRATION
Pour tout réel aet h6=0,
f(a+h)−f(a)
h=k−k h=0
fest donc dérivable en aet f0(a)=0.
16 Première S4 – 2016/2017

COURS DÉRIVATION DES FONCTIONS
Fonctions affines
Théorème 3.3
Si fest la fonction définie sur Rpar : f(x)=mx +p
alors fest dérivable sur Ret pour tout réel x:f0(x)=m.
DÉMONSTRATION
Pour tout réel aet h6=0,
f(a+h)−f(a)
h=m(a+h)+p−ma −p h=mh h=m
fest donc dérivable en aet f0(a)=m
Fonction carré
Théorème 3.4
Si fest la fonction définie sur Rpar : f(x)=x2
alors fest dérivable sur Ret pour tout réel x:f0(x)=2x.
DÉMONSTRATION
Pour tout réel aet h6=0,
f(a+h)−f(a)
h=(a+h)2−a2 h=2ah +h2 h=2a+h
De plus, 2a+htend vers 2alorsque htend vers 0. fest donc dérivable en aet f0(a)=2a.
Fonctions puissances
Théorème 3.5
Soit nun entier tel que nÊ1.
Si fest la fonction définie sur Rpar : f(x)=xn
alors fest dérivable sur Ret pour tout réel x:f0(x)=nxn−1.
Résultat admis.
Fonction inverse
Théorème 3.6
Si fest la fonction définie sur ]−∞;0[∪]0;+∞[par : f(x)=1
x
alors fest dérivable sur ]−∞;0[et sur ]0;+∞[et pour tout x6= 0 : f0(x)=− 1
x2
Première S4 – 2016/2017 17

DÉRIVATION DES FONCTIONS COURS
DÉMONSTRATION
Pour tout réel a6=0 et h6=0,
f(a+h)−f(a)
h=
1
a+h−1 a
h=a−(a+h) ha(a+h)=−1 a(a+h)
Or −1
a(a+h)tend vers −1 a2lorsque htend vers 0.
fest donc dérivable en aet f0(a)= − 1
a2
Fonction racine carrée
Théorème 3.7
Si fest la fonction définie sur [0;+∞[par : f(x)=px
alors fest dérivable sur ]0;+∞[et pour tout réel x>0 : f0(x)=1
2px.
DÉMONSTRATION
Pour tout réel a>0 et h6= 0 tel que a+h>0,
f(a+h)−f(a)
h=pa+h−pa h=(pa+h−pa)(pa+h+pa)
h(pa+h+pa)
=a+h−a
h(pa+h+pa)=1
pa+h+pa
Or, lorsque htend vers 0, 1
pa+h+patend vers 1
2pa
fest donc dérivable en aet f0(a)=1
2pa
3.2.3 Opérations sur les fonctions et dérivées
uet vdésignent deux fonctions dérivables sur un intervalle Iet kun réel.
Théorème 3.8
La fonction u+vest dérivable sur Iet (u+v)0=u0+v0.
La fonction ku est dérivable sur Iet (ku)0=ku0.
DÉMONSTRATION
Pour tout a∈Iet h6=0 tel que a+h∈I:
(u+v)(a+h)−(u+v)(a)
h=u(a+h)+v(a+h)−u(a)−v(a) h
=u(a+h)−u(a)
h+v(a+h)−v(a) h
dont la limite est u0(a)+v0(a) lorsque htend vers 0.
18 Première S4 – 2016/2017

COURS DÉRIVATION DES FONCTIONS
(ku)(a+h)−(ku)(a)
h=ku(a+h)−ku(a) h=ku(a+h)−u(a) h
dont la limite est ku0(a) lorsque htend vers 0.
Exemple Calculer la dérivée de la fonction f définie sur ]0;+∞[par f (x)=3x2+1
3x−5px+2
fest dérivable sur ]0;+∞[car elle est la somme de fonctions dérivables sur ]0;+∞[
et, pour tout x∈]0;+∞[,f0(x)=3×2x+1
3×µ−1 x2¶−5×1
2pxainsi :
f0(x)=6x−1
3x2−5
2px
Théorème 3.9
La fonction uv est dérivable sur Iet (uv)0=u0v+uv0.
La fonction u2est dérivable sur Iet (u2)0=2uu0.
DÉMONSTRATION
Pour tout a∈Iet h6=0 tel que a+h∈I:
(uv)(a+h)−(uv)(a)
h=u(a+h)v(a+h)−u(a)v(a+h)+u(a)v(a+h)−u(a)v(a) h
=u(a+h)−u(a)
h
| {z }
tend vers u0(a)
×v(a+h)+v(a+h)−v(a)
h
| {z }
tend vers v0(a)
×u(a)
dont la limite est u0(a)v(a)+v0(a)u(a) lorsque htend vers 0.
Ainsi uv est dérivable et (uv)0=u0v+uv0.
Exemple Calculer la dérivée de la fonction f définie sur Rpar f (x)=(x2+1)(x5+2)
f(x)=u(x)v(x) avec u(x)=x2+1 et v(x)=x5+2.
fest donc dérivable sur Ren tant que produit de fonctions dérivables sur Ret
f0(x)=2x(x5+2)+5x4(x2+1)
Théorème 3.10
Si vne s’annule pas sur I
La fonction 1
vest dérivable sur Iet µ1 v¶0=− v0 v2
La fonction u
vest dérivable sur Iet ³u v´0=u0v−uv0 v2
Première S4 – 2016/2017 19