Document

Rappels : Loi de Bernouilli et loi binomiale
I) Loi de Bernoulli
Def : une épreuve de Bernoulli est une expérience aléatoire qui n’a que deux issues possibles :
l’une appelée « succès » S qui a pour probabilité p, et l’autre appelée « échec » qui a pour
probabilité 1 – p. La variable aléatoire X qui prend la valeur 1 lorsque X est un succès et 0
sinon est appelé variable aléatoire de Bernoulli de paramètre p.La loi de probabilité de
X est appelée loi de Bernoulli de paramètre p:
k 1 0
P(X = k) p 1-p
Propriétés : On considère une variable aléatoire X de Bernoulli, de paramètre p :
E(X) = p V(X) =p(1–p) σ(X) =
√
(v(X))
II) Loi Binomiale.
1°) Définition
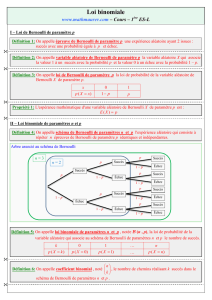
Def : On appelle schéma de Bernoulli d’ordre n,
l’expérience aléatoire qui est la répétition de n
épreuves de Bernoulli identiques et indépendantes.
Def : Le nombre de chemin de l’arbre associé à un
schéma de Bernoulli d’ordre n conduisant à k
succès , pour
n répétitions ,
est noté
(
n
k
)
(coefficient binomial) . ( On lit k parmi n)
TH1 : On considère un schéma de Bernoulli
d’ordre n et de paramètre p ( la probabilité de
chaque succès est donc p). La loi de probabilité de
la variable aléatoire X qui à chaque issue associe le nombre k de succès pour n épreuves est :
P(X = k) =
(
n
k
)
 pk(1– p)n-k
La variable aléatoire X suit une loi binomiale de paramètre n et p.
Rq : Pour n = 1, on retrouve la loi de Bernoulli : P(X=1) =p et p(X=0) =1 – p.
2°) Propriétés des coefficients binomiaux :Pour tout nombre entier n et k :
Si 0 ≤ k ≤ n alors
(
n
n−k
)
=
(
n
k
)
.
Formule de Pascal :Si 0 ≤ k ≤ n -1 alors
(
n
k
)
+
(
n
k+1
)
=
(
n+1
k+1
)
Application : triangle de Pascal
0 1 2 3 4 5
01
111
2121
313 3 1
414 6 41
51510 10 5 1
1

RQ :
(
n
0
)
= 1 et
(
n
1
)
= n
A la calculatrice : irem de Lyon : 36 élèves ; 36 calculatrices
TI : dans le menu Math/probas : 3 nCr 1 ou 3 combinaison 1 correspond à
(
3
1
)
En premier : le nombre de répétition n ;En dernier : le nombre de succès k
3°) Calcul de p(X=k) ou de p(X ≤ k).
a) A la calculatrice :
Pour les TI : 2nde Distr 0binompdf( n , p ,k) pour p(X = k) ou 0binomFdp(n,p,k)
Abinompdf( n , p ,k) pour p(X ≤ k) ou AbinomFrep(n,p,k)
b) Avec le tableur :Exemple B(100 ;0.16)
Pour p(X=k) : on utilise la formule =loi.binomiale( k ;n ;p ;0)
Pour p(X<=k) : on entre la formule=loi.binomiale( k ;n ;p;1).
4°) Exemples :
a. On lance trois fois de suite un dé équilibré et on s’intéresse au nombre de sortie du 6.
On répète ainsi trois fois de suite une épreuve de Bernoulli : »lancer d’un dé cubique » de
paramètre
p=1
6
, un succès étant l’obtention d’un 6.On considère X la variable aléatoire
qui associe le nombre de succès après trois lancers.X prend les valeurs 0,1,2 ou 3.
On reprend l'arbre précédent
k0123
P(X=k) (1 – p) 3 = 0,579 3  p (1 –p)2
=0,069
3  p2 (1 – p) =
0,069
p3 = 0,005
b. On lance 20 fois de suite le même dé et on s’intéresse au nombre de 6. On considère la va-
riable aléatoire X qui s’intéresse au nombre de succès. X suit une loi binomiale B(20;
1
6
).
●Calcul de la probabilité d'obtenir 8 fois le 6 :
p (X = 8) =
(
20
8
)
 (
1
6
)8(
5
6
)12
On peut également le calculer directement à la calculatrice avec la fonction :
2nde Distr 0binompdf( 20 ;
1
6
;8). On trouve 0,0084. La probabilité d'obtenir 8 fois un 6
sur 20 lancers est d'environ 0,8 % .
●Calcul de la probabilité d'obtenir au moins 5 fois le 6 : On cherche
p(X⩾5)
.
p(X⩾5)
=
1−p(X⩽4)
On obtient avec la calculatrice et en utilisant la fonction Abinomcdf( 20 ;
1
6
;4) , la valeur
0,23.
5°) Espérance et Variance. On suppose que X suit une loi binomiale de paramètres n et p
E(X) = np V(X) =np(1-p)
2