Démonstration de la formule de conjugaison pour les miroirs

Démonstration de la formule de conjugaison pour les miroirs sphériques
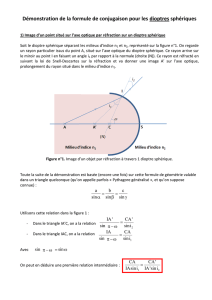
1) Image d’un point situé sur l’axe optique par réflexion sur un miroir sphérique
Soit le miroir sphérique représenté sur la figure n°1. On regarde un rayon particulier issus du point A,
situé sur l’axe optique du miroir sphérique. Ce rayon arrive sur le miroir au point I en faisant un angle
i1 par rapport à la normale (droite (N)) à la droite tangente au miroir (droite (D)) au point I. Ce rayon
est réfléchi en suivant la loi de Snell-Descartes sur la réflexion et va donner une image A’ sur l’axe
optique.
Pour les besoins de la démonstration on a besoin de définir le point T, intersection de la droite (D) et de
l’axe optique du miroir ainsi que les différents angles représentés sur la figure.
Figure n°1. Image d’un objet par réflexion sur un miroir sphérique.
Toute la suite de la démonstration est basée sur cette formule de géométrie valable dans un triangle
quelconque (qu’on appelle parfois « Pythagore généralisé », et qu’on suppose connue) :
a b c
sin sin sin
Avec les angles et les distances définies sur la figure 2.
Figure 2. Triangle quelconque.
Utilisons cette relation dans la figure :
- Dans le triangle IA’C, on a la relation
- Dans le triangle IAC, on a la relation
1
IA' CA'
sin sini
1
IA CA
sin sini

On peut en déduire une première relation intermédiaire :
Changeons de triangles rectangles.
- Dans le triangle TA’I, on a la relation
- Dans le triangle TAI, on a la relation
On se rappellera de deux formules trigo (voir cours lycée) :
D’où on peut en déduire que :
En utilisant les deux relations encadrées, on arrive donc à :
Qui, si on introduit les valeurs algébriques donne la relation :
Introduisons le point C dans cette relation :
Qui, après un peu de mathématique, se met sous la forme :
(c’est la relation de conjugaison du miroir sphérique)
Il est évident que si on regarde un autre rayon partant de A et touchant le miroir en un autre point,
que le point T change de place, et que donc par conséquent A’ va changer lui aussi de place. Donc on a
montré que pour un objet ponctuel, différents rayons partant de A et réfléchis par le miroir ne vont
pas donner la même image. Ceci n’est plus vrai si l’on se place dans certaines conditions, comme on va
le voir ci-dessous.
11
11
IA' CA' IA' sin
sin sini CA' sini IA' IA
et CA' CA
IA CA IA sin
sin sini CA sini
11
TA' IA'
sin sin
ii
22
11
TA IA
sin sin
ii
22
1
1
sin cosi
i
2
1
111
1
111
TA' IA' TA' cosi
cosi IA'
sin sin
ii
22
TA' TA
et IA' IA
TA IA TA cosi
cosi IA
sin sin
ii
22
TA' CA'
TA CA
TA' CA'
TA CA
TC CA' CA'
TC CA CA
1 1 2
CA' CA CT

2) Image d’un point situé sur l’axe optique dans les conditions de Gauss
On voit que dans le triangle rectangle CTI, on a la relation :
Or CI est le rayon de courbure du miroir sphérique. CS l’est aussi. Donc CI=CS.
On peut donc dire que
Or les conditions de Gauss imposent de choisir des rayons peu inclinés par rapport à l’axe optique.
Ainsi l’angle doit être faible si l’on se place dans ces conditions.
Or lorsque est faible, cos ≈ 1, donc
Donc la relation de conjugaison du miroir sphérique dans l’approximation de Gauss se met sous la
forme :
Et l’on voit bien que, dans ces conditions, lorsque je fixe ma distance CA (object ponctuel), alors
comme CS est une constante, alors CA’ sera lui aussi fixe. Je forme donc dans ces conditions une
image, et une seule, peu importe le rayon choisi. On dit que l’on est dans les conditions de
stigmatisme approché.
CI CTcos
CS
CT cos
CT CS
1 1 2
CA' CA CS