l`angle saillant aob et l`angle rentrant aob

CHAPITRE 15 :ANGLES INSCRITS DANS UN CERCLE
POLYGONES REGULIERS
I) ANGLES INSCRITS DANS UN CERCLE.
1) Définitions.
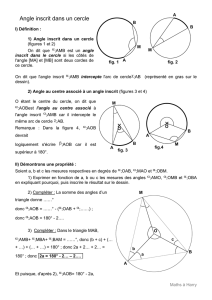
A, B et M désignent trois points d’un cercle (C) centre O. (C)
• On dit que AMB est inscrit dans (C) : son sommet M
appartient à (C) et [MA] et [MB] sont des cordes de (C).
• Des deux arcs du cercle (C) d’extrémités A et B, celui
qui ne contient pas M est appelé arc intercepté par
l’angle inscrit AMB.
• L’angle saillant AOB et l’angle rentrant AOB sont appelés angles au centre de (C) :
son sommet est le centre de (C) et [OA] et {OB] sont des rayons de (C).
• Angle au centre associé à l’angle inscrit AMB :
Cas où l’angle inscrit AMB est aigu Cas où l’angle inscrit AMB est obtus
L’angle saillant AOB est l’angle au centre L’angle rentrant AOB est l’angle au centre
associé à l’angle inscrit AMB. associé à l’angle inscrit AMB.
Remarque : on dit que l’angle inscrit AMB et son angle au centre associé interceptent
le même arc de cercle AB.

2) Propriété de l’angle inscrit.
Dans un cercle, la mesure d’un angle inscrit est égale à la moitié de la mesure de
l’angle au centre associé.
Exemples :
Cas où l’angle inscrit AMB est aigu Cas où l’angle inscrit AMB est obtus
AOB = 2 AMB AOB = 2 AMB
3) Conséquences.
a) Triangle rectangle et cercle.
Propriété : Si un triangle est inscrit dans un cercle ayant pour diamètre un
côté de ce triangle alors ce triangle est rectangle.
Démonstration :
L’angle saillant AÔB et l’angle inscrit AMB
interceptent le même arc AB. Donc AÔB = 2 × AMB.
Comme l’angle au centre AÔB est plat, AÔB = 180°.
Donc AMB = 1
2 AÔB = 180 2 = 90°.
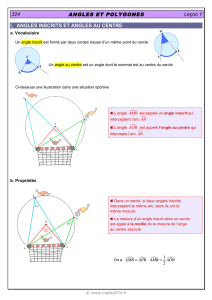
b) Angles inscrits interceptant le même arc.
Propriété : Dans un cercle, si deux angles inscrits interceptent le même arc,
alors ces angles sont égaux.
Démonstration : (cas où les angles inscrits sont aigus)
Les angles inscrits ALB et AMB interceptent le même arc AB.
Donc : ALB = 1
2 AOB et AMB = 1 2 AOB.
Donc ALB = AMB.

II) POLYGONES REGULIERS.
1) Définition.
Un polygone régulier est un polygone dont tous les côtés ont la même longueur et
dont tous les angles ont la même mesure.
Exemple :
Un triangle équilatéral est un
polygone régulier à trois côtés.
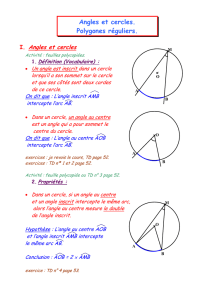
2) Propriété et définitions.
Tout polygone régulier est inscriptible dans un cercle.
Ce cercle est appelé cercle circonscrit au polygone régulier.
Le centre O de ce cercle est appelé le centre du polygone régulier.
Exemple :
3) Dernière propriété.
Soit A et B, deux sommets consécutifs d’un polygone régulier à n côtés de centre O.
Chaque angle au centre, tel AOB, du polygone régulier a une mesure égale à 360°
n.
Exemple : Triangle équilatéral ABC et son cercle circonscrit
AOB = 360°
3 = 120°
Chaque angle au centre, tel AOB, mesure 120° :
BOC = AOC = 120°.

4) Autres exemples de polygones réguliers.
Carré ABCD Pentagone régulier ABCDE
et son cercle circonscrit et son cercle circonscrit
AOB = 360°
4 = 90° AOB = 360° 5 = 72°
Chaque angle au centre, tel AOB, Chaque angle au centre, tel AOB,
mesure 90°. mesure 72°.
Hexagone régulier ABCDEF Octogone régulier
et son cercle circonscrit et son cercle circonscrit
AOB = 360°
6 = 60° AOB = 360° 8 = 45°
Chaque angle au centre, tel AOB, Chaque angle au centre, tel AOB,
mesure 60°. mesure 45°.