Feuille PC1

(Xn) (Yn)Xn→X Yn→Y Xn+Yn
X+Y
(Xn) (Yn)X Y
Xn→X, Yn
P
→c,
c(Xn, Yn) (X, c)
(Xn+Yn)X+c XnYncX
(X1, X2, . . . , X2n+1) 2n+ 1 [0,1] Yn
(Yn) 1/2
(Yn−1/2)
Yn
(2n+ 1)2n
nxn(1 −x)n1x∈[0,1].
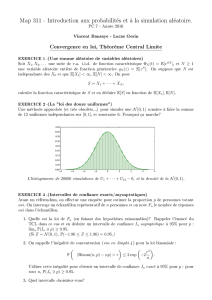
gn
Zn= 2√2n(Yn−1/2)
ZnN(0,1)
Zngn
(gn)g(Zn)
g
X1, . . . , XnXi∼f(· − θ)f
Rµk=RRxkf(x)dx k = 2
k= 4 ¯ Xn=1
nPn
i=1 Xi1
nPn
i=1(Xi−¯
Xn)2
Xi
θ= 0
Sn=1
nPn
i=1 X2
i¯
Xn

θ
nˆ θn
nˆ θn
ˆ
θn
P(N > 1.64) = 5% N∼ N(0,1) εnn θ
P(θ≥ˆ θn+εn)n→∞ →5%
εnθ ε0
n
nˆ θnP(θ≥ˆ θn+ε0
n)n→∞
→5%
(Xn)nσ2>0
Zn=1
σ√n
n
X
j=1
Xj.
t∈Rlimn→+∞E[eitZn] = e−t2
2
(Zn)
Z2n−Zn
(Zn)Z∞
(Z2n−Zn)