Chapitre 6: Fonctions trigonométriques

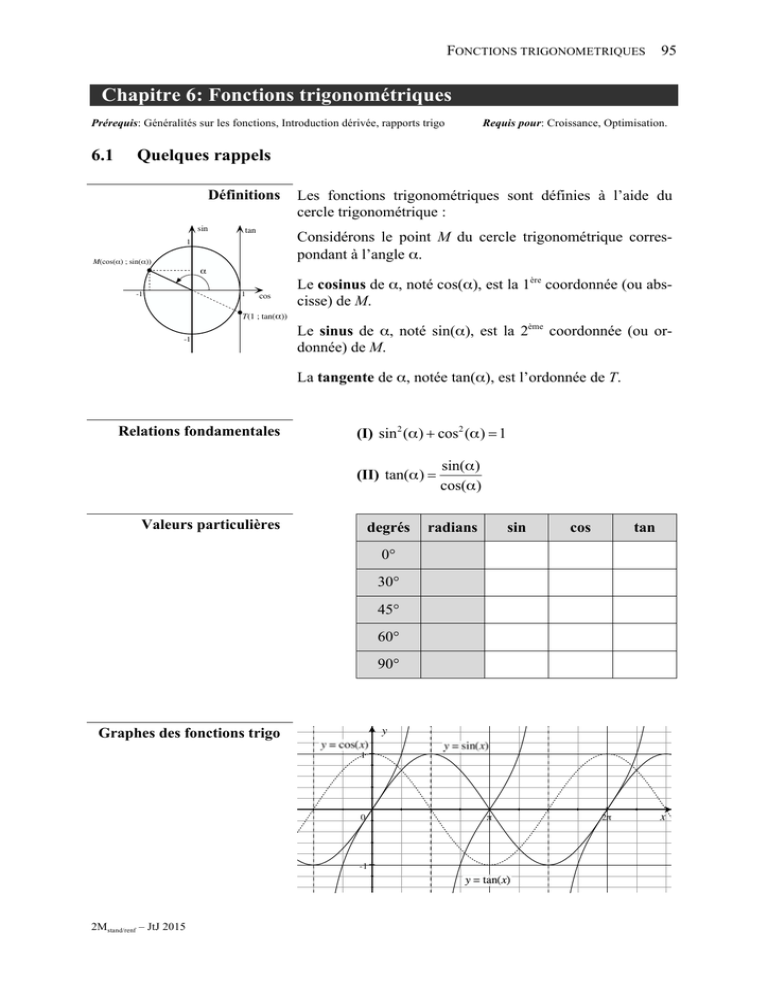
FONCTIONS TRIGONOMETRIQUES
95
Chapitre 6: Fonctions trigonométriques
Prérequis: Généralités sur les fonctions, Introduction dérivée, rapports trigo
6.1
Requis pour: Croissance, Optimisation.
Quelques rappels
Définitions
Les fonctions trigonométriques sont définies à l’aide du
cercle trigonométrique :
Considérons le point M du cercle trigonométrique correspondant à l’angle α.
Le cosinus de α, noté cos(α), est la 1ère coordonnée (ou abscisse) de M.
Le sinus de α, noté sin(α), est la 2ème coordonnée (ou ordonnée) de M.
La tangente de α, notée tan(α), est l’ordonnée de T.
Relations fondamentales
(I) sin 2 (α) + cos2 (α) = 1
(II) tan(α) =
Valeurs particulières
degrés
sin(α)
cos(α)
radians
sin
cos
tan
0°
30°
45°
60°
90°
Graphes des fonctions trigo
2Mstand/renf – JtJ 2015
96
CHAPITRE 6
Périodicité
• La fonction sinus est périodique de période ……
sin(α + …) = sin(…)
• La fonction cosinus est périodique de période ……
cos(α + …) = cos(…)
• La fonction tangente est périodique de période ……
tan(α + …) = tan(…)
Exemple
⎛ x⎞
a) Esquisser la fonction f (x) = 3sin⎜ ⎟ puis préciser sa
⎝ 2⎠
période et son amplitude.
2Mstand/renf – Jt 2015
FONCTIONS TRIGONOMETRIQUES
Exemple
Exercice 6.1 :
1
b) Esquisser la fonction f (x) = − cos( x + π) puis préciser
2
sa période, son amplitude.
Esquisser les fonctions suivantes en précisant sa période,
son amplitude:
⎛ x⎞
a) f (x) = −2cos⎜ ⎟
⎝ 3⎠
⎛
π⎞
b) f (x) = sin⎜ x + ⎟
2⎠
⎝
⎛x ⎞
c) f (x) = 3cos⎜ + π ⎟
⎝2 ⎠
Théorème
Si f (x) = a ⋅ sin(bx + c) ou f (x) = a ⋅ cos(bx + c) ,
où a, b et c sont des réels non nuls, alors :
•
•
2Mstand/renf – JtJ 2015
97
l’amplitude A vaut : | a |
2π
la période T vaut :
|b|
98
CHAPITRE 6
Exemple
⎛x ⎞
On considère la fonction f définie par f (x) = −3cos⎜ + π ⎟ .
⎝2 ⎠
Déterminer l’amplitude A et la période T de f. En déduire
son esquisse
Exercice 6.2 :
Pour chacune des fonctions suivantes, déterminer sa période T et son amplitude A :
⎛
π⎞
a) f (x) = sin⎜ x − ⎟
2⎠
⎝
b) g(x) = 2cos( 3x + π )
⎛ x π⎞
c) h(x) = −cos⎜ + ⎟
⎝ 2 3⎠
d) i(x) = −2sin( 3x − π)
Retrouver sur le graphe ci-dessous les courbes correspondantes à ces 4 fonctions :
2Mstand/renf – Jt 2015
FONCTIONS TRIGONOMETRIQUES
6.2
99
Quelques équations trigonométriques
Introduction
Exemple
Exercice 6.3 :
Une équation trigonométrique est une équation contenant
des expressions trigonométriques. Il n’existe pas de méthode universelle, mais le cercle trigonométrique sera très
souvent votre allié.
Résoudre cos(2x) = -0,9
Résoudre les équations suivantes (en degrés):
a) cos(x) = −
2Mstand/renf – JtJ 2015
1
2
b) sin(3x) = 0,829
c) tan(x) = −0,754
d) cos(−x) = −1,43
⎛ x⎞
e) tan⎜ ⎟ = 5,33
⎝ 2⎠
f) sin(3x) = −
3
2
100
CHAPITRE 6
Exemple
Exercice 6.4 :
Exemple
⎛
3
π⎞
Résoudre sin⎜2x + ⎟ = −
⎝
2⎠
2
Résoudre les équations suivantes (en radians):
⎛
π⎞ 1
a) sin⎜ x + ⎟ =
⎝
4⎠ 2
⎛
π⎞ 1
b) cos⎜ x − ⎟ =
⎝
3⎠ 2
⎛
π⎞ 1
c) sin⎜2x − ⎟ =
⎝
3⎠ 2
⎛
2
π⎞
d) cos⎜ 4 x − ⎟ =
⎝
4⎠ 2
e) tan(2x + π) = 3
⎛ x⎞
f) tan⎜ ⎟ = −1
⎝ 2⎠
Résoudre sin 2 ( x ) = 1
2Mstand/renf – Jt 2015
FONCTIONS TRIGONOMETRIQUES
Exercice 6.5 :
Exemple
Exercice 6.6 :
Résoudre les équations suivantes (en radians):
a) cos2 ( x ) = 1
b) sin 2 ( x ) =
1
4
c) tan 2 ( x ) = 3
d) sin 2 ( x ) =
3
4
e) tan 2 ( x ) = 1
f) sin 2 (x) = cos2 (x)
Résoudre 4 cos2 (x) − 4 cos(x) − 3 = 0
Résoudre les équations suivantes (en degrés):
a) 2sin 2 (x) − 5sin(x) + 2 = 0
b) 2cos2 (x) − 3cos(x) + 1 = 0
c) tan 2 (x) + 2tan(x) = −1
2Mstand/renf – JtJ 2015
101
102
CHAPITRE 6
Exemple
Exercice 6.7 :
Résoudre 3sin 2 (x) + cos2 (x) − 2 = 0
Résoudre les équations suivantes (en degrés):
a) 3sin 2 (x) + cos2 (x) − 2 = 0
b) 2cos2 (x) − sin(x) = 1
c) 5sin(x) = 6cos 2 (x)
2Mstand/renf – Jt 2015
FONCTIONS TRIGONOMETRIQUES
6.3
103
Dérivée des fonctions trigonométriques
Introduction
À l'image des chapitres précédents, nous pourrions déterminer la dérivée de la fonction f (x) = sin(x) à l’aide du calcul
sin(x) − sin(a)
.
de limite : lim
x→a
x−a
Essayons de trouver cette dérivée en comparant les graphes
de f (x) et de la pente de la tangente en plusieurs points.
2
y
f (x) = sin(x)
−π
π
2π
x
π
2π
x
−2
1
y
−π
−1
f (x) = . . . . . . . . .
Des démarches analogues permettraient de justifier les
règles suivantes :
Les règles de dérivation des fonctions trigo :
8ème règle : Si f (x) = sin(x)
⇒
f ′(x) = cos(x)
9ème règle : Si f (x) = cos(x)
⇒
f ′(x) = −sin(x)
10ème règle : Si f (x) = tan(x)
⇒
Exercice 6.8 :
2
Dériver les fonctions suivantes :
a) f (x) = sin(x) + cos(x)
c) f (x) = cos(x) – 2tan(x)
e) f (x) =
2Mstand/renf – JtJ 2015
f ′(x) = ( tan(x)) +1
1
ou f ′(x) =
2
(cos(x))
sin(x)
1+ cos(x)
b) f (x) = x2 · cos(x)
tan(x)
x
x
f) f (x) =
sin(x) + cos(x)
d) f (x) =
104
CHAPITRE 6
Exercice 6.9 :
En combinant les règles 8 et 9 du tableau précédent, justifier
la 10ème règle (sous les deux formes).
Exercice 6.10 :
Déterminer l’équation de la tangente à la courbe au point
indiqué :
a) f (x) = tan(x) au point d’abscisse x = π
b) f (x) = x cos(x) au point d’abscisse x = π
Exercice 6.11 :
6.4
En quelles valeurs de x ∈ [ 0; 2π ] , la courbe y = x + 2sin(x)
a-t-elle une tangente horizontale ?
La dérivée de fonctions composées
Introduction
Nous avons déjà eu l’occasion de dériver quelques fonctions
composées ; en effet les fonctions :
• f (x) = x − 2 correspond à f (x) = (g h)(x) avec
g(x) = ……… et h(x) = ………
• f (x) = (3x − 5)3 correspond à f (x) = (g h)(x) avec
g(x) = ……… et h(x) = ………
• f (x) =
1
3
x2 + 4
correspond à f (x) = (g h)(x) avec
g(x) = ……… et h(x) = ………
Lors du calcul de ces 3 dérivées, nous avons vu apparaître
ce que nous avons appelé la dérivée interne. Ceci se généralise lors du calcul de la dérivée de toutes les fonctions
composées.
Les règles de dérivation des fonctions composées :
11ème règle : Si f (x) = sin( g(x))
⇒
f ′(x) = cos( g(x)) ⋅ g′(x)
12ème règle : Si f (x) = cos( g(x))
⇒
f ′(x) = −sin( g(x)) ⋅ g′(x)
13ème règle : Si f (x) = tan( g(x))
⇒
f ′(x) =
1
(cos(g(x)))
2
⋅ g′(x) =
g′(x)
(cos(g(x)))
2
ou plus généralement pour toutes les fonctions composées :
14ème règle : Si f (x) = g(x) h(x) = g(h(x))
⇒
f ′(x) = g′(h(x)) ⋅ h′(x)
2Mstand/renf – Jt 2015
FONCTIONS TRIGONOMETRIQUES
Exemple
dériver les 2 fonctions suivantes :
a) f (x) = sin( x 2 )
b) f (x) = (sin(x))
Exercice 6.12 : Dériver les fonctions suivantes :
a) f (x) = tan(3x)
b) f (x) = cos(x 3 )
d) f (x) = x sin 1x
c) f (x) = cos 3 (x)
2Mstand/renf – JtJ 2015
2
105
106
CHAPITRE 6
2Mstand/renf – Jt 2015