Limites, asymptotes, nombre dérivé, fonction dérivée

1
LE TALENT C’EST D’AVOIR ENVIE
En partenariat avec :
© Tous droits réservés Studyrama 2010
Fiche téléchargée sur www.studyrama.com
MATHEMATIQUES Série ES
Nº : 22003
Fiche Cours
Plan de la che
I - Nombre dérivé
II - Interprétation graphique du nombre dérivé, tangente à une courbe
III - Fonction dérivée, règles de dérivation
I - Nombre dérivé
f
C
étant la courbe représentative d’une fonction f, dénie sur
f
E
, soit a un réel donné de
f
E
et x un réel variable de
f
E
. Notons
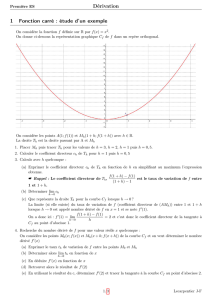
A (a; f (a)) et M (x = a + h ; f (x) = f (a + h)) les points de
f
C
correspondants (cf. gure 5).
Fig. 5 Vers le nombre dérivé...
DÉFINITION
On dit que f est dérivable en a si :
h
)a()ha(
lim
0h
ff −+
→
(
ax
)a()x(
lim
ax −
−
=→
ff
) est un réel (donc non inni), unique (que x
tende vers a par valeurs inférieures ou supérieures à a). Ce réel, s’il existe, est noté f’ (a) et est dit nombre dérivé de
f en a.
Exemple :
Soit f telle que f (x) =
2
x
;
h
)a()ha(
lim
0h
ff −+
→
0h
lim
→
=
=
−+
h
a)ha( 22
…
0h
lim
→
=
(2 a + h) = 2 a (noter que cette limite avait un aspect
initial indéterminé, du type
0
0
). Ainsi f est bien dérivable en a, et pour toute valeur a de IR – le nombre 2 a existant pour tout réel
a – le nombre dérivé est f’(a) = 2 a.
Thème : Limites, asymptotes, nombre dérivé, fonction dérivée
Fiche 3 : Nombre dérivé, tangente à une courbe, fonction dérivée, règles de dérivation

2
LE TALENT C’EST D’AVOIR ENVIE
En partenariat avec :
© Tous droits réservés Studyrama 2010
Fiche téléchargée sur www.studyrama.com
MATHEMATIQUES Série ES
Nº : 22003
Fiche Cours
► À SAVOIR
•Si
h
)a()ha(
lim
0h
ff −+
→
(
ax
)a()x(
lim
ax −
−
=→
ff
) n’existe pas ou est innie on dit que f n’est pas dérivable en a.
• On dit que f est dérivable sur un intervalle D de IR si elle est dérivable en tout « point » a de D. On retiendra à ce
propos que tout polynôme est dérivable sur IR, toute fonction rationnelle (rapport de deux polynômes) est dérivable
sur son ensemble de dénition.
II - Interprétation graphique du nombre dérivé, tangente à une courbe
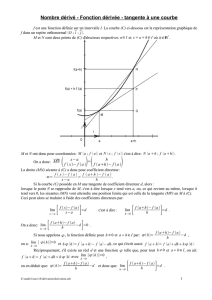
Fig. 6 Le nombre dérivé : coefcient directeur de la tangente en A
Quand h tend vers 0, M se rapproche inniment près de A. La corde (AM) tend alors à se confondre avec la tangente (
A
T
) (en A)
à
f
C
, si cette tangente existe. Or le rapport
h
)a()ha( ff −+
est, précisément, le coefcient directeur de la corde (AM). On peut
donc comprendre que le nombre dérivé
=
−+
→h
)a()ha(
lim
0h
ff
f’(a) n’est autre que le coefcient directeur de la tangente en A.
On admettra sans autre démonstration la règle ci-dessous.
RÈGLE
Si une fonction f est dérivable en a,
f
C
admet en A (a ; f (a)) une tangente (
A
T
), unique et non verticale, de coefcient
directeur m = f’ (a). Et réciproquement.
III - Fonction dérivée, règles de dérivation
DÉFINITION
Lorsqu’une fonction f est dérivable en a, a ∈
f
E
, le nombre dérivé est noté f’(a) ; cette notation signie qu’il existe,
associée à f, une (autre) fonction notée f’ qui, à l’antécédent a, associe l’image f’(a) ; f’ est la fonction dérivée de f.
Exemple :
Quand on a f (x) =
2
x
, on a vu que f’(a) = 2 a : ceci se résume en disant que f est dérivable sur IR (car 2 a existe pour tout réel a)
et sa dérivée est la fonction f’ dénie par f’(x) = 2 x.

3
LE TALENT C’EST D’AVOIR ENVIE
En partenariat avec :
© Tous droits réservés Studyrama 2010
Fiche téléchargée sur www.studyrama.com
MATHEMATIQUES Série ES
Nº : 22003
Fiche Cours
Dérivées usuelles et intervalles de dérivabilité :
f (x) f’(x) D
constante 0 IR
n
x
, n ∈ IN
1n
xn −
IR
1/ x -1/
2
x
IR*
x
1/(2
x
)
*
RI +
Sin x Cos x IR
Cos x – Sin x IR
Tan x
( )2
xnat1 +
x ≠ π/2 [?]
Tab. 2 Dérivées usuelles
RÈGLES
Règles de dérivation
u et v sont deux fonctions dérivables sur D, k une constante, n un entier naturel. Les résultats suivants sont à connaître
par cœur !
• f (x) = k · u (x) , f’(x) = k · u’ (x), ∀ x, x ∈ D
• f (x) = u (x) + v (x), f’(x) = u’(x) + v’(x), ∀ x, x ∈ D
• f (x) = u (x) × v (x), f’(x) = u’(x) · v(x) + u (x) · v’ (x), ∀ x, x ∈ D
• f (x) =
n
u
(x), f’(x) = nu’(x)
1n
u
−
(x), ∀ x, x ∈ D
(cas particulier très fréquent : f (x) =
2
u
(x), f’(x) = 2 u’(x) u (x), ∀ x, x ∈ D)
• f (x)
)x(u=
, f’(x) =
)x(u2
)x('u
, ∀ x, x ∈ D et tel que u (x) > 0
• f (x) =
)x(v
1
, f’(x) =
)x(v
)x('v
2
−
, ∀ x, x ∈ D, et tel que v (x) ≠ 0
• f (x) =
)x(v
)x(u
, f’(x) =
)x(v
)x('v)x(u)x(v)x('u
2
−
, ∀ x, x ∈ D, et tel que v (x) ≠ 0
Dérivée d’une fonction composée : le résultat énoncé ci-dessous est particulièrement important en terminale :
Si f (x) = u [v (x)], on note symboliquement f = u ○ v, alors f’(x) = v’(x) · u’[v (x)]
(toutes les conditions sur les intervalles d’existence et de dérivabilité étant satisfaites).
Exemples :
• f (x) =
n
v
(x) (soit f = u ○ v, avec u : x
n
x
), n ∈ IN. Donc f’(x) = v’(x) · n ·
[ ] 1n
)x(v −
(où l’on retrouve le 4e résultat des règles de dérivation ci-dessus).
• f (x)
)x(v=
(soit f = u ○ v, avec u : x
x
) . Donc f’(x) =
)x(v2
)x('v
)x(v2
1
)x('v =×
(où l’on retrouve le 5e résultat des règles
de dérivation ci-dessus)
► À SAVOIR
Un cas usuel important : si v est afne, c’est-à-dire que v (x) = ax + b, on obtient : f’(x) = a · u (ax + b).
Exemple : f (x) = sin (2 x – 3), alors f’(x) = 2 cos (2 x – 3), (u = sin, v (x) = 2 x – 3).