Outils mathématiques pour la physique (PCSI) Dérivées successives d'une fonction scalaire d'une variable réelle — Wikiversité

Wikiversité
Outils
mathématiques
pour la physique
(PCSI)/Dérivées
successives d'une
fonction scalaire
d'une variable réelle
< Outils mathématiques pour la physique (PCSI)

......Soit la fonction scalaire de la
variable réelle continue et dérivable
en toute valeur d'un intervalle de
définition.
......Notions vues dans le secondaire.
Continuité d'une fonction
......La fonction est dite continue en
si, quand , admet une
limite égale à soit
Rappel des notions de
continuité et dérivabilité de
fonction

.
Dérivabilité d'une fonction
......La fonction est dite dérivable en
si existe, sa
valeur définissant soit
[1];
......la fonction est dite dérivable sur un
domaine de dérivabilité si son nombre
dérivé existe pour toutes les valeurs du
domaine.
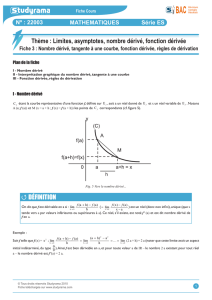
......Propriétés du nombre dérivé: Le
nombre dérivé est le cœfficient directeur

(ou pente) de la tangente du graphe de
en fonction de au point
d'abscisse , l'équation de la tangente
s'écrivant
,
......Propriétés du nombre dérivé: c'est
encore la tangente de l'angle orienté
que fait la tangente du graphe de
en fonction de au point d'abscisse
, avec l'axe des abscisses soit,
.
Définition
Dérivabilité du second ordre

......La fonction est dite dérivable en
au 2e ordre si
existe, sa valeur définissant ,
soit
[2].
Propriétés
......La valeur du nombre dérivé du
second ordre traduit la façon dont la
dérivée première varie avec la variable,
une valeur positive correspondra à une
«croissance de la dérivée première»[3]
alors qu'une valeur négative
correspondra à une «décroissance»[4].