Primitives d`une fonction continue sur un intervalle

LEÇON N˚ 76 :
Primitives d’une fonction continue sur un
intervalle; définition et propriétés de
l’intégrale, inégalité de la moyenne.
Applications.
Pré-requis :
–Si fest une fonction numérique dérivable sur ]a, b[telle que f′= 0 (resp. >0), alors fest constante
(resp. croissante);
–Si f∈C0[a, b], alors f[a, b]est un intervalle fermé borné.
Approche intuitive
Soit fune fonction continue et positive sur I= [a, b](avec a < b)
et Csa courbe représentative dans un repère othonormal. Pour x0∈
[a, b], on note A(x)l’aire qui est délimitée par l’axe des abscisses, C
et les droites d’équations x=aet x=x0.
Pour tout x0∈I,
h f(x0)6A(x0+h)−A(x0)6hg(x0) + ε
⇔f(x0)61
hA(x0+h)−A(x0)6f(x0) + ε
h→0(⇒ε→0)
⇒A′(x0) = f(x0).
Donc A′=fsur l’intervalle I.
Ox0x0+h
C
f(x0)
f(x0) + h
A(x0+h)
−A(x0)
76.1 Primitives d’une fonction continue
Définition 1 : Soit f:I⊂R−→ R. On dit qu’une fonction F:I−→ Rest une primitive de fsur
Isi Fest dérivable et F′=f.
Théorème 1 : Soit f:I−→ Rcontinue. Alors fadmet au moins une primitive sur I.
Remarque 1 :Ce théorème est admis.

2Primitives d’une fonction, intégrale, inégalité de la moyenne
Théorème 2 : Soit f:I−→ Rcontinue admettant pour primitive F. Alors {x7→ F(x)+c, c ∈R}
est l’ensemble des primitives de fsur I. De plus, si x0∈Iet y0∈R, alors il existe une unique
primitive Gde fsur Itelle que G(x0) = y0.
démonstration :Fest dérivable sur I, donc pour tout c∈R,x7→ F(x) + cl’est aussi sur I. Posons
alors e Fc(x) = F(x)+c. Alors e F′
c(c)+F′(x) = f(x), donc e
Fcest une primitive de fsur I. De plus, si e Fc
et e Fc′sont deux primitives telles que e
Fc(x0) = e Fc′(x0) = y0, alors en particulier, F(x)+c=F(x)+c′,
d’où c=c′.
Corollaire 1 : Soit f:I−→ Rcontinue admettant pour primitive F. Pour toute primitive Gde f
sur Icontenant aet b,F(a)−F(b) = G(a)−G(b).
démonstration :Il existe une contante c∈Rtelle que pour tout réel x∈I, on a G(x) + F(x) + c,
donc G(a)−G(b) = F(a) + c−F(b) + c=F(a)−F(b).
76.2 Recherche d’une primitive
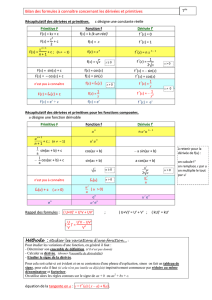
76.2.1 Tableau inverse de dérivées
I
(n∈N)
⊂R
(n>2)
⊂R⊂R∗
+⊂R⊂R⊂R\{π
2[π]}
f(x)xnx−n1/√xcos xsin x1 + tan2x= cos−2x
F(x)xn+1
n+ 1
x1−n
1−n2√xsin x−cos xtan x
76.2.2 Propriétés usuelles
Soient uet vadmettant pour primitives Uet Vsur I. Alors :
⋄ ∀ α, β ∈R,αu +βv admet pour primitive αU +βV ;
⋄ ∀ a6= 0,x7→ u(ax +b)admet pour primitive 1
aU(ax +b);
⋄ ∀ n∈N,u·Unadmet pour primitive Un+1
n+ 1.
Si vadmet pour primitive Vsur J⊂Rtel que U(I)⊂J, alors V◦Uest une primitive de u·(v◦U)sur I.
76.3 Définition et propriétés de l’intégrale
Définition 2 : Soient f:I−→ Rcontinue et a, b ∈I(a6b). On appelle intégrale de aàbde fle
nombre F(b)−F(a), noté Rb
af(t) dtou F(t)b
a, où Fest une primitive de fsur I.
Remarques 2 :
– Cette définition ne dépend pas de la primitive choisie (corollaire 1).
– On a en particulier Ra
af(t) dt=F(a)−F(a) = 0 et Rb
af(t) dt=−Ra
bf(t) dt.

Primitives d’une fonction, intégrale, inégalité de la moyenne 3
Théorème 3 : Soit f:I−→ Rcontinue. La fonction Fdéfinie sur Ipar F(x) = Rx
af(t) dt(a∈I)
est LA primitive de fsur Is’annulant en a.
démonstration :fadmet une primitive G. Alors Rx
af(t) dt=F(x) = G(x)−G(a). Donc F′(x) =
G′(x) = f(x)pour tout x∈I, d’où Fest bien une primitive de f. Or F(a) = F(a)−G(a) = 0, donc
d’après le théorème 2, Fest l’unique primitive de fs’annulant en a.
Exemple : Soit f:R∗
+−→ Rla fonction définie par f(x) = 1
x. Alors
F(x) = Zx
1
f(t) dt=Zx
1
dt
t= ln(x).
Proposition 1 : soient f, g :I−→ Rcontinues. Alors :
(i) Pour tous a, b, c ∈I, on a Rc
af(t) dt=Rb
af(t) dt+Rc
bf(t) dt(relation de Chasles);
(ii) Pour tous a, b ∈Iet pour tous α, β ∈R, on a Rb
aαf(t) + βg(t) dt=αRb
af(t) dt+
βRb
ag(t) dt.
démonstration :
(i) Puisque fest continue sur I, elle admet une primitve Fsur I. Il vient que
Zb
a
f(t) dt+Zc
b
f(t) dt=F(b)−F(a) + F(c)−F(b) = F(c)−F(a) = Zc
a
f(t) dt.
(ii) Si Fet Gdésignent des primitives de fet gsur I, alors les propriétés du paragraphe 2.2 nous
assurent que αF +βG est une primitive de αf +βg. Donc
Zb
a
αf(t) + βg(t) dt=αF (b) + βG(b)−αF (a)−βG(a)
=αF(b)−F(a)−βG(b)−G(a)
=αZb
a
f(t) dt+βZb
a
g(t) dt,
d’où le résultat demandé. 
Proposition 2 : Soit f:I−→ Rcontinue et positive. Alors pour tous a, b ∈Itels que a6b, on a
Rb
af(t) dt>0.
démonstration :Soit Fune primitive de fsur I. Alors F′=f>0, donc Fest croissante. Par suite,
F(b)>F(a)⇔F(b)−F(a)>0⇔Zb
a
f(t) dt>0.
Proposition 2’ : Soit f:I−→ Rcontinue et positive telle qu’il existe x0∈Itel que f(x0)6= 0.
Alors pour tous a, b ∈Ivérifiant a6b, on a Rb
af(t) dt > 0.

4Primitives d’une fonction, intégrale, inégalité de la moyenne
démonstration :fest continue signifie qu’il existe [c, d]⊂[a, b](c < d)tel que pour tout x∈,¸d],
f(x)> f(x0)/2. Alors
Zb
a
f(t) dt=Zc
a
f(t) dt
|{z }
>0
+Zd
c
f(t) dt+Zb
d
f(t) dt
|{z }
>0
>Zd
c
f(t) dt > 1
2Zd
c
f(x0) dt=f(x0)
2(d−c)>0.
Corollaire 2 : Soient f, g :I−→ Rcontinues telles que f6gsur I. Alors pour tous a, b ∈I
vérifiant a6b, on a Rb
af(t) dt6∈b
ag(t) dt.
démonstration :On a par hypothèse g−f>0sur I, donc
Zb
a
g(t)−f(t) dtprop 1 =Zb
a
g(t) dt−Zb
a
f(t) dt>0,
d’où le résultat. 
Corollaire 3 : Soit f:I−→ Rcontinue. Pour tous a, b ∈I, on a |Rb
af(t) dt|6Rb
a|f(t)|dt.
démonstration :Rappelons que pour tous x, y ∈R,|x| − |y|6|x+y|6|x|+|y|(il s’agit de
l’inégalité triangulaire). Sur I, posons f+= sup(f, 0) et f−= sup(−f, 0), de sorte que f=f+−f−
et |f|=f++f−. D’après la proposition 2, f+, f−>0⇒Rb
af+,Rb
af−>0, donc
Zb
a
f=Zb
a
f+−f−=Zb
a
f+−Zb
a
f−
6Zb
a
f++Zb
a
f−=Zb
a
f++Zb
a
f−prop 1
=Zb
a
f++f−
Zb
a
f6Zb
a|f|.
Exercice :
– Montrer que pour tous x, y ∈R,|sin x−sin y|6|x−y|.
– Soient a, b ∈Itels que a < b, et
n:C0([a, b]) −→ R
f7−→ Rb
a|f(t)|dtet ϕ:C0([a, b])2−→ R
(f, g)7−→ Rb
af(t)g(t) dt.
Montrer que nest une norme sur C0([a, b]) et que ϕest un produit scalaire.
Solution :
– Soient x, y ∈R. On peut supposer, quitte à échanger leurs rôles, que x6y. Pour tout t∈R, on a :
−16cos t61coro 2 ⇔Zy
x
−1 dt6Zy
x
cos(t) dt6Zy
x
1 dt⇔[−t]y
x6[sin(t)]y x6[t]y x⇔ | sin x−sin y|6|x−y|.
– Rappelons tout d’abord qu’une norme sur un R-espace vectoriel Eest une application Nà valeurs positives et satisfaisant les
critères de séparation, d’homogénéité et d’inégalité triangulaire. nest déjà une application à valeurs positives. Vérifions alors
les autres points :

Primitives d’une fonction, intégrale, inégalité de la moyenne 5
Séparation : Soit f∈C0([a, b]) tel que n(f) = 0. Montrons alors par l’absurde que f= 0. Supposons donc que f6= 0.
Il existe alors x0∈[a, b]tel que f(x0)6= 0, et la proposition 2’ nous assure alors que Rb
af(t) dt > 0. En appliquant
ensuite le corollaire 3, on obtient l’inégalité suivante :
0<Zb
a
f(t) dt=Zb
a
f(t) dt6Zb
a
|f(t)|dt.
Ceci implique alors que n(f)>0, ce qui contredit l’hypothèse de départ. On obtient donc bien l’implication n(f) = 0 ⇒
f= 0.
Homogénéité : Soient λ∈Ret f∈C0([a, b]). Alors
n(λf) = Zb
a
|λf(t)|dt=Zb
a
|λ|·|f(t)|dt=|λ|Zb
a
|f(t) dt=|λ|n(f).
Inégalité triangulaire : Soient enfin f, g ∈C0([a, b)]. Alors
n(f+g) = Zb
a
|f(t) + g(t)|dtcoro 2 6Zb
a
|f(t)|+|g(t)|dt=Zb
a
|f(t)|dt+Zb
a
|g(t)|dt=n(f) + n(g).
Rappelons ensuite qu’une application est un produit scalaire si elle est bilinéaire, symétrique, positive et séparée. Vérifions
ces quatre points pour l’application ϕ:
Positivité : Soit f∈C0([a, b]). Montrons que ϕ(f, f )>0:ϕ(f, f) = Rb
af(t)2dtprop 2
>0.
Séparation : Soit f∈C0([a, b]). Montrons par l’absurde que ϕ(f, f ) = 0 ⇒f= 0. Supposons que f6= 0, c’est-à-dire qu’il
existe x0∈[a, b]tel que f(x0)6= 0. Alors f(x0)26= 0, et la proposition 2’ nous assure que Rb
af(t)2dt > 0, ou encore
ϕ(f, f )>0, ce qui contredit l’hypothèse de départ. Par conséquent, il vient que f= 0.
Bilinéarité : Cette propriété ne sera vérifiée que pour f, les rôles de fet gétant symétriques dans ϕ. Supposons gconstante.
Alors pour tous f1, f2∈C0([a, b]) et λ∈R, on a
ϕ(f1+f2, g) = Zb
af1(t) + f2(t)g(t) dt=Zb
a
f1(t)g(t) + f2(t)g(t) dt=Zb
a
f1(t)g(t) dt+Zb
a
f2(t)g(t) dt
=ϕ(f1, g) + ϕ(f2, g),
et ϕ(λf1, g) = Zb
aλf1(t)g(t) dt=λZb
a
f1(t)g(t) dt=λϕ(f1, g).
Symétrie : La symétrie est assurée par la commutativité du produit dans R:f(t)g(t) = g(t)f(t).
Théorème 4 (inégalité de la moyenne) : Soient f:I−→ Rcontinue et a, b ∈Ivérifiant a < b. S’il
existe deux réels met Mtels que m6f6Msur I, alors m(b−a)6Rb
af(t) dt6M(b−a).
démonstration :Pour tout x∈I,
f(x)−m>0prop 2 ⇒Zb
a
f(t)−mdt>0⇔Zb
a
mdt6Zb
a
f(t) dt⇔m(b−a)6Zb
a
f(t) dt.
On montre de la même manière que Rb
af(t) dt6M(b−a).
76.4 Applications
Exercice : Calculer l’aire entre une parabole (x7→ x2) et une sécante entre les deux points d’intersection.