Séquence 7. Trigonométrie

I. RAPPELS DE SECONDE
1 ) ORIENTATION DU PLAN
Définition :
Dans le plan muni d'un repère (O,I,J) et orienté positivement, le cercle trigonométrique est le cercle de
centre O et de rayon 1.
Soit
D
la tangente au cercle trigonométrique au point I et K le point de
D
de coordonnées (1;1). (I,K) est donc un repère de
l'axe
D
.
Par le procédé de l'enroulement de
D
autour du cercle :
–à tout point de l'axe
D
d'abscisse x, correspond un point M du cercle.
–tout point du cercle est associé à une infinité de points de l'axe, donc à une infinité de nombres réels.
Propriété :
Soit x un réel, et M le point du cercle trigonométrique associé au réel x, alors le point M est associé à tous les réels de la forme
x+k×2π,
avec k entier.
En d'autres termes,les points de
D
d'abscisses....,
x−4
,
x−2π
,
x+2π
,
x+4π
, , etc... se retrouvent également en M
après enroulement du cercle.
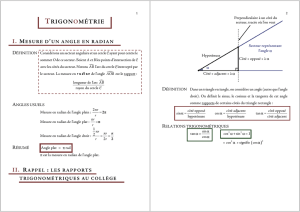
2 ) MESURE DES ANGLES EN RADIAN
Définition :
Soit K le point de D d’abscisse 1.
Par enroulement de D autour du cercle, on lui associe le point R telle que la longueur de l'arc IR est égale à 1.
Le radian (
rad
) est la mesure de l'angle géométrique
I
̂
OR
qui intercepte, un arc de longueur 1 sur le cercle trigonométrique.
Propriété :
La mesure d'un angle en radians est proportionnelle à sa mesure en degré.
Le tableau ci-dessous fournit les mesures remarquables :
mesures en degré 180 360 45 30
mesures en radian
2
3
•1
rad
≈
57,3 ° 1° =
180
rad
≈
0,0175
rad
Par convention, le sens positif est le sens inverse de celui des aiguilles d'une
montre : il est appelé sens direct ou sens trigonométrique.
Conséquence : Soit A et B deux points du cercle trigonométrique, la
mesure en radians de l'angle AOB est égale à la longueur de l'arc
intercepté AB.
Séquence 7. Trigonométrie

3) COSINUS ET SINUS D'UN ANGLE
Définition :
Soit M le point du cercle trigonométrique associé au réel x.
• l'abscisse du point
M
est le cosinus de
x
( noté
cos x
)
• l'ordonnée
yM
du point
M
est le sinus de
x
( noté
sin x
)
Exemples :
cos 0=1
et
sin 0 =0
;
cos  =−1
et
sin  = 0
;
cos 
2=0
et
sin 
2=1
;
cos –
2
=0
et
sin –
2
=–1
VALEURS REMARQUABLES DU SINUS ET DU COSINUS
x
(en
degré)
0 30 45 60 90
x
(en
radian)
0
6
4
3
2
sin
x
0
1
2
2
2
3
2
1
cos
x
1
3
2
2
2
1
2
0
Propriétés :
Pour tout réel
x
, on a :
•
∀k∈ℤ
,
cos ( x+2kπ ) =......
et
sin ( x+2kπ ) =........
•
......⩽cos
x
.....
et
.....
sin
x
....
•
sin2x+cos2x=....
•
cos ( −x ) =......
et
sin ( −x ) =......

II. MESURES D'UN ANGLE ORIENTÉ DE VECTEURS
1) ANGLE ORIENTÉ DE DEUX VECTEURS NON NULS
Définition :
Le plan est muni d'un repère orthonormé direct (O,I,J).
Soit
⃗u
et
⃗v
deux vecteurs non nuls.
On construit sur le cercle trigonométrique les points A et B tel que
⃗
OA
soit colinéaire et de même sens que
⃗u
et
⃗
OB
soit
colinéaire et de même sens que
⃗v
. Alors :
–La mesure de l'angle orienté (
⃗u
,
⃗v
) est égale à celle de l'angle orienté (
⃗
OA
,
⃗
OB
).
–Pour tout réel a associé au point A et tout réel b associé au point B,
b−a
est une mesure en radian de l'angle orienté
(
⃗
OA
,
⃗
OB
).
Concrètement, une mesure de l'angle orienté (
⃗
OA
,
⃗
OB
) en radian est égale à la longueur de l'arc
̂
AB
, à un multiple de
2π
près.
Remarque : Si
b−a
et une mesure en radian de l'angle orienté (
⃗
OA
,
⃗
OB
) alors les mesures de cet angle orienté sont tous
les réels
b−a+2k π.
On note :(
⃗
OA
,
⃗
OB
) =
b−a+2k π=b−a(2π).
Attention : l'ordre est important ! (
⃗
OB
,
⃗
OA
) = - (
⃗
OA
,
⃗
OB
)
Exemple : Dans le plan muni d'un repère orthonormé direct (O, I, J ), on considère le dodécagone régulier direct
ABCDEFGHKLMN.
1) Déterminer une mesure positive en radian de chacun des angles orientés suivants :
(
⃗
OA
,
⃗
OB
) =
(
⃗
OA
,
⃗
OE
) =
(
⃗
OA
,
⃗
OH
) =
2) Déterminer une mesure négative en radian des angles orientés suivants :
(
⃗
OA
,
⃗
OD
) =
(
⃗
OA
,
⃗
OK
) =
3) Déterminer une mesure en radian des angles orientés suivants :
(
⃗
OB
,
⃗
OE
) =
(
⃗
OK
,
⃗
OG
) =
4 ) Que dire du triangle GOF ? En déduire la mesure en radian de (
⃗
GO
,
⃗
GF
).
5 ) Quelle est la mesure de l'angle (
⃗
AG
,
⃗
AE
) ?
voir savoir faire : exercice 13 p. 239
N
M
L
K
H
G
F
E
D
C
B
A
O
I
J

2) MESURE PRINCIPALE D'UN ANGLE ORIENTÉ DE VECTEURS
Définition :
Parmi toutes les mesures en radian d'un angle orienté(
u , v
), il en existe une seule appartenant à
l'intervalle
] −π ;π ]
.
On l'appelle mesure principale de l’angle orienté (
u , v
).
Remarque :
La valeur absolue de la mesure principale de l’angle orienté (
u , v
)est la mesure de l’angle géométrique formé par ces deux
vecteurs.
Exemple :
•
20
3π=(...+... 3) π=.... 3+...×2π;
la mesure principale est …..
•
107
6π=.......
La mesure principale est …... et l'angle géométrique associé a pour mesure …..................
Remarque : Soit A et B deux points du cercle trigonométrique. La mesure principale de l'angle (
⃗
OA
,
⃗
OB
) est égale
à la longueur du plus court chemin partant de A et allant vers B, affecté du signe – si on s'est déplacé dans le sens
indirect.
3) PROPRIÉTÉ DES ANGLES ORIENTÉS
Propriété : angle nul ou plat :
Soit
⃗
u
et
⃗
v
deux vecteurs non nuls :
1) Si
⃗
u
et
⃗
v
sont colinéaires et de même sens,
(⃗ u ,⃗ v)=0(2π)
.
2) Si
⃗
u
et
⃗
v
sont colinéaires et de sens contraires,
(⃗ u ,⃗ v)=π(2π)
.
Propriété : relation de Chasles sur les vecteurs
Soit
⃗
u
,
⃗
v
, et
⃗
w
trois vecteurs non nuls :
(⃗ u ,⃗ v)+ (⃗ v , ⃗ w)=(⃗ u , ⃗ w)(2π)
.
Exemple :
ABCD est un carré. Construire le point E tel que DEB est un triangle isocèle.
(
⃗
DC
,
⃗
DE
) = (
⃗
DC
,
⃗
DB
) + (…..., ….)
(2π)
=
π
4+....(2π)=....(2π)
(
⃗
DE
,
⃗
DA
) = ….........................................................................................................
Conséquences de la Relation de Chasles :
A B
CD