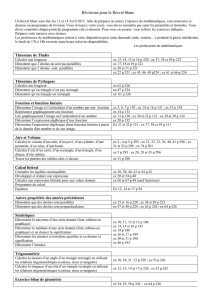
Comment démontrer que deux droites sont parallèles

La démonstration en
mathématiques
Le but de cette étude est de découvrir
une méthode pour réaliser des
démonstrations

Avec un exemple…
Soit une droite (u) et deux points A et B de (u) . Par A tracer
la droite (d) perpendiculaire à (u) et par B la droite (d’)
perpendiculaire à (u) .
Que peut-on dire des droites (d) et (d’) ?
A B
(u)
(d) (d’)

(u) A B
(d) (d’)
BUT :
A (u)
B (u)
INFORMATIONS
Donc (d) // (d’)
Conclusion
A (d)
(d) (u)
B (d')
(d') (u)
(d) // (d’)

Pour construire une démonstration, l’ouvrier mathématicien a
besoin d’outils
Ces théorèmes nombreux
sont réunis sur des fiches par
thème
Laquelle de ces fiches contient-elle le précieux
théorème ?
Fiche :Comment démontrer qu’un triangle est isocèle
Fiche :Comment démontrer que deux distances sont
égales
Fiche :Comment démontrer que deux droites sont
perpendiculaires
Fiche :Comment démontrer qu’un quadrilatère est un
rectangle
Fiche :Comment démontrer que deux droites sont
parallèles
Fiche :Comment démontrer que deux distances sont
égales
Fiche :Comment démontrer qu’un triangle est rectangle
(u) AB
(d) (d’)
BUT : (d) // (d’)
C’est bien cette
fiche .
Quels théorèmes
contient-elle ?
Ces outils portent entre autres le nom de
théorèmes
INFOS
A (u)
B (u)
(d) (u)
B (d’)
(d’) (u)
A (d)

(u) AB
(d) (d’)
Comment démontrer que deux droites
sont parallèles
Si deux droites sont symétriques par rapport à
un point alors elles sont parallèles .
Si deux droites déterminent avec une sécante
des angles alternes-internes de même mesure alors
elles sont parallèles
Si deux droites déterminent avec une sécante
des angles alternes-externes de même mesure alors
elles sont parallèles
Si deux droites déterminent avec une sécante
des angles correspondants de même mesure alors
elles sont parallèles
Si un quadrilatère est un trapèze alors ses
bases sont parallèles
Si un quadrilatère est un parallélogramme
alors ses côtés opposés sont parallèles
Si deux droites sont parallèles à une même
droite alors elles sont parallèles
Si deux droites sont perpendiculaires à une
même droite alors elles sont parallèles
Quel théorème
semble être le
mieux adapté à
ce problème ?
C’est sûrement le bon
théorème .
Observons le
BUT : (d) // (d’)
INFOS
A (u)
B (u)
(d) (u)
B (d’)
(d’) (u)
A (d)