Comment démontrer que deux droites sont parallèles ?

COMMENT DEMONTRER QUE DEUX DROITES SONT PARALLELES ?
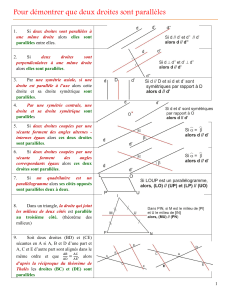
1) En utilisant le parallélisme à une troisième droite :
Deux droites parallèles à une même droite sont
parallèles entre elles.
(d
2
) est parallèle à (d
1
)
et (d
3
) est parallèle à (d
1
)
donc (d
2
) est parallèle à (d
3
)
2) En utilisant la perpendicularité à une troisième droite :
Deux droites perpendiculaires à une même droite
sont parallèles entre elles.
(d
2
) est perpendiculaire à (d
1
)
et (d
3
) est perpendiculaire à (d
1
)
donc (d
2
) est parallèle à (d
3
)
3) En utilisant des angles formés par deux droites et une sécante :
Deux droites formant avec une troisième droite des angles alternes-internes ou correspondants de
même mesure sont parallèles.
a
yAt eta uCz sont des angles alternes-
internes et ont la même mesure donc les
droites (xy) et (uv) sont parallèles.
a
yAt et a vCt sont des angles correspondants
et ont la même mesure donc les droites (xy)
et (uv) sont parallèles.
4) En utilisant un parallélogramme (ou parallélogramme particulier) :
Les côtés opposés d’un parallélogramme sont parallèles.
ABCD est un parallélogramme donc ses côtés opposés [AB] et [DC]
sont parallèles. De même, [AD] et [BC] sont parallèles.
5) En utilisant le théorème des milieux :
Dans un triangle, la droite passant par les milieux de deux côtés est parallèle au troisième côté.
Exemple : I est le milieu de [AB] et J est le milieu de
[BC] donc d’après l’un des théorèmes des milieux, la
droite (IJ) est parallèle à la droite (AC).

6) En utilisant une propriété de la symétrie centrale :
L’image d’une droite par une symétrie centrale est une droite parallèle.
(d’) est l’image de (d) par la symétrie de centre
O donc (d) et (d’) sont parallèles.
7) En utilisant la réciproque du théorème de Thalès :
Exemple :
AB
AM = 35 40 et AC AN = 21 24 (CALCULS SEPARES)
1
ère
méthode : (si les rapports « tombent juste »)
AB
AM = 35 40 = 0,875 et AC AN = 21 24 = 0,875
donc AB
AM = AC AN
2
ème
méthode (simplification de fraction) :
AB
AM = 35 40 = 7×5
8×5 = 7
8 et AC AN = 21 24 = 7×3
8×3 = 7
8
donc AB
AM = AC AN
3
ème
méthode (produit en croix) :
35 × 24 = 840
40 × 21 = 840
donc AB
AM = AC AN
de plus les points A,B et M sont alignés dans le même ordre que les points A,C et N
donc d’après la réciproque du théorème de Thalès, les droites (BC) et (MN) sont parallèles.