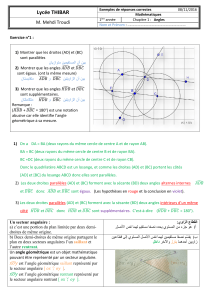
Comment démontrer que deux droites sont parallèles ?

1
Pour démontrer que deux droites sont parallèles
1. Si deux droites sont parallèles à
une même droite alors elles sont
parallèles entre elles.
2. Si deux droites sont
perpendiculaires à une même droite
alors elles sont parallèles.
3. Par une symétrie axiale, si une
droite est parallèle à l’axe alors cette
droite et sa droite symétrique sont
parallèles.
4. Par une symétrie centrale, une
droite et sa droite symétrique sont
parallèles
5. Si deux droites coupées par une
sécante forment des angles alternes -
internes égaux alors ces deux droites
sont parallèles.
6. Si deux droites coupées par une
sécante forment des angles
correspondants égaux alors ces deux
droites sont parallèles.
7. Si un quadrilatère est un
parallélogramme alors ses côtés opposés
sont parallèles deux à deux.
8. Dans un triangle, la droite qui joint
les milieux de deux côtés est parallèle
au troisième côté. (théorème des
milieux)
9. Soit deux droites (BD) et (CE)
sécantes en A si A, B et D d’une part et
A, C et E d’autre part sont alignés dans le
même ordre et que 
, alors
d’après la réciproque du théorème de
Thalès les droites (BC) et (DE) sont
parallèles