Aucun titre de diapositive

EM
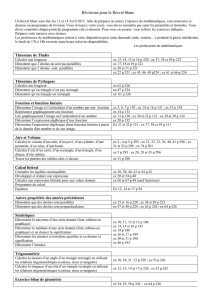
L’unité est le centimètre. La figure n ’est pas à l ’échelle .
On ne demande pas de reproduire la figure.
Les points E,M,A,B sont alignés dans cet ordre, les points F,P,A,C
sont alignés dans cet ordre.
Les droites (EF) et (MP) sont parallèles.
AM = 6 ; MP = 4,8 ; AP = 3,6 ; EF = 6 ; AC = 4,5 ; AB = 7,5
1) Démontrer que le triangle AMP est un triangle rectangle.
2) Calculer AE et en déduire la longueur ME.
3) Démontrer que les droites (MP) et (BC) sont parallèles.
4) Démontrer que les angles CBA et AMP sont égaux.
FP
A
C
B

Le côté le plus long du triangle AMP
est AM = 6 cm.
Je compare
AM² = 6²
AM² = 36
AP² + MP² = 3,6² + 4,8²
AP² + MP² = 12,96 + 23,04
AP² + MP² = 36
D’après le théorème réciproque de
Pythagore ce triangle est rectangle en A.
1) Le triangle AMP est-il rectangle ?
EM
FP
A
C
B
6
4,8 3,6
Les mesures des trois côtés sont
connues.
On cherche à savoir si l ’égalité de
Pythagore est vérifiée.
L’égalité de Pythagore est
vérifiée : on applique le
théorème réciproque de
Pythagore.

EM
FP
A
C
B
EM
FP
A
C
B
6
4,8 3,6
6
Les droites (MP) et (EF) sont parallèles donc les triangles
AMP et AEF sont en situation de THALES.
L’égalité de THALES s ’écrit :
AE
AM
AF
AP
EF
MP
2) On demande de calculer AE et EM.
Sur ce croquis on sait que les droites (MP) et (EF) sont parallèles.
On connaît AM = 6 AP = 3,6 MP = 4,8 et EF = 6 .
Petit côté
grand côté parallèle
Petit côté
grand côté parallèle
Petit côté
grand côté parallèle
A est le point opposé aux deux côtés parallèles.

AE
AM
AF
AP
EF
MP
68,46,36  AFAM
Pour calculer MN je choisis
68,46  AM
4,8 AM = 36
: 4,8 AM = 36/4,8
AM = 7,5 cm
Les points A,M et E sont alignés donc EM =AE - AM donc EM =1,5cm
EM
FP
A
C
B
EM
FP
A
C
B
6
4,8 3,6
6

EM
FP
A
C
B
6
3,6
4,5
7,5
3) Démontrer que les droites (MP) et (BC) sont parallèles.
Les points M,A,B d ’une part et les points P,A et C d ’autre part sont
alignés dans le même ordre, donc si
AM
AP
AB
AC
Alors les droites (MP) et (BC) sont parallèles.
Je vérifie
AM
AP
6,0
66,3 
AB
AC
6,0
5,7 5,4 
L’égalité est vérifiée donc les droites (MP) et (BC) sont parallèles
d’après le théorème réciproque de THALES.