Synthèse des modèles

Formation des enseignants
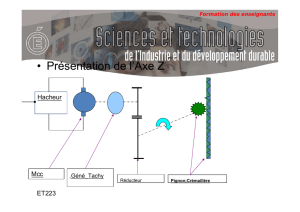
ET223
•Tableau des
Analogies
domaine Effort Flux Déplace
ment
électrique Tension
(V) Courant (A) Charge (q)
Méca
translation force (N) Vitesse (m/s) déplace
ment
(m)
Méca
rotation Couple (Nm) Vitesse (rd/s) Angle (rd)
Hydrauliqu
ePression
(P) Débit Vol (m3/s) Volume (m3)
•Analogie mécanique de la
résistance
dt
dq
Ru 
dt
dx
F
Frottement visqueux
Analogie mécanique de l’inductance
2
2
dtqd
Lu 
2
2
dt xd
mF 
Analogie mécanique capacité
2
2
2
2
2
1
;
2
1
dt
dx
mE
dt
dq
LE cm 
)(.;
1rappeldeforcexkFq
C
u
22 2
1
;
1
2
1kxEq
C
Epes 

Formation des enseignants
ET223
»LIAISON SYSTEME/MODELE
•Équation
différentielle
•Fonction de
transfert
)(pF
y(t)
Y(p)
x(t)
X(p)
entrée sortie

Formation des enseignants
ET223
•Système Intégrateur pur
•Équation différentielle
•Équation de la sortie
x y
)(. txk
dt
dy 
tdttxky
0
)(.
La sortie y(t) est proportionnelle à l’intégrale de l’entrée x(t)

Formation des enseignants
ET223
p
K
pX pY
pG  )( )( )(
2
)()( p
KE
pY
p
E
pX 
Fonction de transfert
Réponse indicielle
X(t)=échelon d’amplitude E
tKEty .)( 
Modèle intégrateur pur
table

Formation des enseignants
ET223
Intégrateur pur
Diagramme de BODE
Module:
K
jG log20)( 
Phase
2
))(arg( jG